“Accelerating ADMM for efficient simulation and optimization” by Zhang, Peng, Ouyang and Deng
Conference:
Type(s):
Title:
- Accelerating ADMM for efficient simulation and optimization
Session/Category Title: Accelerated Physics
Presenter(s)/Author(s):
Moderator(s):
Abstract:
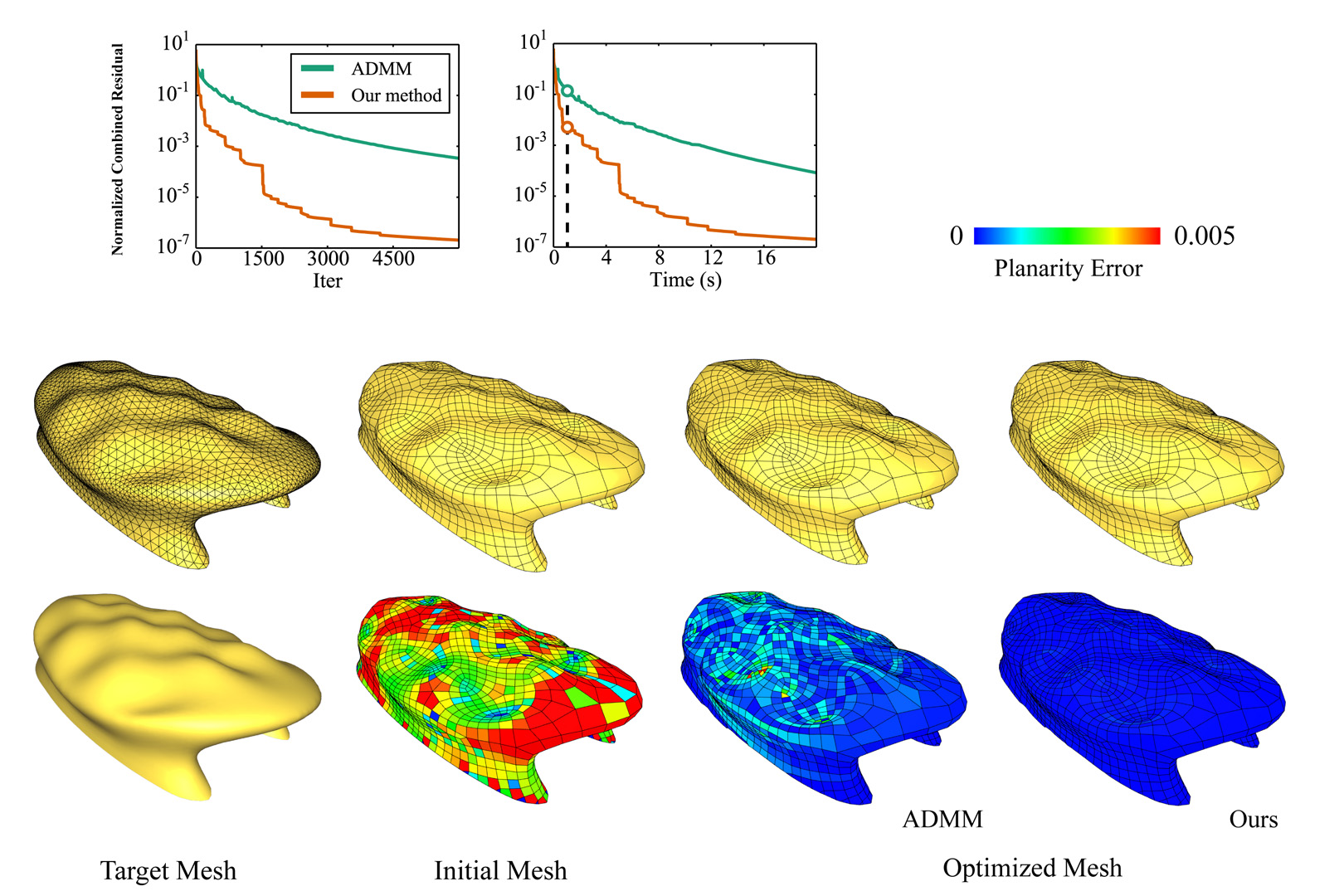
The alternating direction method of multipliers (ADMM) is a popular approach for solving optimization problems that are potentially non-smooth and with hard constraints. It has been applied to various computer graphics applications, including physical simulation, geometry processing, and image processing. However, ADMM can take a long time to converge to a solution of high accuracy. Moreover, many computer graphics tasks involve non-convex optimization, and there is often no convergence guarantee for ADMM on such problems since it was originally designed for convex optimization. In this paper, we propose a method to speed up ADMM using Anderson acceleration, an established technique for accelerating fixed-point iterations. We show that in the general case, ADMM is a fixed-point iteration of the second primal variable and the dual variable, and Anderson acceleration can be directly applied. Additionally, when the problem has a separable target function and satisfies certain conditions, ADMM becomes a fixed-point iteration of only one variable, which further reduces the computational overhead of Anderson acceleration. Moreover, we analyze a particular non-convex problem structure that is common in computer graphics, and prove the convergence of ADMM on such problems under mild assumptions. We apply our acceleration technique on a variety of optimization problems in computer graphics, with notable improvement on their convergence speed.
References:
1. M. S. C. Almeida and M. Figueiredo. 2013. Deconvolving images With unknown boundaries using the alternating direction method of multipliers. IEEE Transactions on Image Processing 22, 8 (2013), 3074–3086.Google ScholarCross Ref
2. Donald G. Anderson. 1965. Iterative procedures for nonlinear integral equations. J. ACM 12, 4 (1965), 547–560.Google ScholarDigital Library
3. Sofien Bouaziz, Mario Deuss, Yuliy Schwartzburg, Thibaut Weise, and Mark Pauly. 2012. Shape-Up: Shaping discrete geometry with projections. Comput. Graph. Forum 31, 5 (2012), 1657–1667.Google ScholarDigital Library
4. Sofien Bouaziz, Sebastian Martin, Tiantian Liu, Ladislav Kavan, and Mark Pauly. 2014. Projective dynamics: fusing constraint projections for fast simulation. ACM Trans. Graph. 33, 4 (2014), 154:1–154:11.Google ScholarDigital Library
5. Sofien Bouaziz, Andrea Tagliasacchi, and Mark Pauly. 2013. Sparse iterative closest point. Computer Graphics Forum 32, 5 (2013), 113–123.Google ScholarDigital Library
6. Stephen Boyd, Neal Parikh, Eric Chu, Borja Peleato, Jonathan Eckstein, et al. 2011. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine learning 3, 1 (2011), 1–122.Google Scholar
7. Christopher Brandt, Elmar Eisemann, and Klaus Hildebrandt. 2018. Hyper-reduced projective dynamics. ACM Trans. Graph. 37, 4 (2018), 80:1–80:13.Google ScholarDigital Library
8. S. H. Chan, X. Wang, and O. A. Elgendy. 2017. Plug-and-play ADMM for image restoration: Fixed-point convergence and applications. IEEE Transactions on Computational Imaging 3, 1 (2017), 84–98.Google ScholarCross Ref
9. R. Chartrand. 2012. Nonconvex splitting for regularized low-rank + sparse decomposition. IEEE Transactions on Signal Processing 60, 11 (2012), 5810–5819.Google ScholarDigital Library
10. R. Chartrand and B. Wohlberg. 2013. A nonconvex ADMM algorithm for group sparsity with sparse groups (ICASSP 2013). 6009–6013.Google Scholar
11. S. Claici, M. Bessmeltsev, S. Schaefer, and J. Solomon. 2017. Isometry-Aware preconditioning for mesh parameterization. Comput. Graph. Forum 36, 5 (2017), 37–47.Google ScholarDigital Library
12. Patrick L. Combettes and Jean-Christophe Pesquet. 2011. Proximal splitting methods in signal processing. In Fixed-Point Algorithms for Inverse Problems in Science and Engineering, Heinz H. Bauschke, Regina S. Burachik, Patrick L. Combettes, Veit Elser, D. Russell Luke, and Henry Wolkowicz (Eds.). 185–212.Google Scholar
13. Bailin Deng, Sofien Bouaziz, Mario Deuss, Alexandre Kaspar, Yuliy Schwartzburg, and Mark Pauly. 2015. Interactive design exploration for constrained meshes. Computer-Aided Design 61, Supplement C (2015), 13–23.Google ScholarDigital Library
14. Wei Deng and Wotao Yin. 2016. On the global and linear convergence of the generalized alternating direction method of multipliers. Journal of Scientific Computing 66, 3 (2016), 889–916.Google ScholarDigital Library
15. Jonathan Eckstein and Dimitri P Bertsekas. 1992. On the Douglas—Rachford splitting method and the proximal point algorithm for maximal monotone operators. Mathematical Programming 55, 1–3 (1992), 293–318.Google ScholarCross Ref
16. T. Erseghe, D. Zennaro, E. Dall’Anese, and L. Vangelista. 2011. Fast consensus by the alternating direction multipliers method. IEEE Transactions on Signal Processing 59, 11 (2011), 5523–5537.Google ScholarDigital Library
17. Claire Evans, Sara Pollock, Leo G. Rebholz, and Mengying Xiao. 2018. A proof that Anderson acceleration improves the convergence rate in linearly converging fixed point methods (but not in those converging quadratically). arXiv preprint arXiv:1810.08455 (2018).Google Scholar
18. V. Eyert. 1996. A comparative study on methods for convergence acceleration of iterative vector sequences. J. Comput. Phys. 124, 2 (1996), 271–285.Google ScholarDigital Library
19. Haw-ren Fang and Yousef Saad. 2009. Two classes of multisecant methods for nonlinear acceleration. Numerical Linear Algebra with Applications 16, 3 (2009), 197–221.Google ScholarCross Ref
20. M. A. T. Figueiredo and J. M. Bioucas-Dias. 2010. Restoration of Poissonian images using alternating direction optimization. IEEE Transactions on Image Processing 19, 12 (2010), 3133–3145.Google ScholarDigital Library
21. Michel Fortin and Roland Glowinski. 1983. Chapter III On Decomposition-Coordination Methods Using an Augmented Lagrangian. In Studies in Mathematics and Its Applications. Vol. 15. Elsevier, 97–146.Google Scholar
22. Daniel Gabay and Bertrand Mercier. 1976. A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Computers & Mathematics with Applications 2, 1 (1976), 17–40.Google ScholarCross Ref
23. Akash Garg, Andrew O. Sageman-Furnas, Bailin Deng, Yonghao Yue, Eitan Grinspun, Mark Pauly, and Max Wardetzky. 2014. Wire mesh design. ACM Trans. Graph. 33, 4 (2014), 66:1–66:12.Google ScholarDigital Library
24. E. Ghadimi, A. Teixeira, I. Shames, and M. Johansson. 2015. Optimal parameter selection for the alternating direction method of multipliers (ADMM): quadratic problems. IEEE Trans. Automat. Control 60, 3 (2015), 644–658.Google ScholarCross Ref
25. P. Giselsson and S. Boyd. 2017. Linear convergence and metric selection for Douglas-Rachford splitting and ADMM. IEEE Trans. Automat. Control 62, 2 (2017), 532–544. T. Goldstein, B. O’Donoghue, S. Setzer, and R. Baraniuk. 2014. Fast alternating direction optimization methods. SIAM Journal on Imaging Sciences 7, 3 (2014), 1588–1623. James Gregson, Ivo Ihrke, Nils Thuerey, and Wolfgang Heidrich. 2014. From capture to simulation: Connecting forward and inverse problems in fluids. ACM Trans. Graph. 33, 4 (2014), 139:1–139:11.Google ScholarCross Ref
26. D. Hajinezhad, T. Chang, X. Wang, Q. Shi, and M. Hong. 2016. Nonnegative matrix factorization using ADMM: Algorithm and convergence analysis (ICASSP 2016). 4742–4746.Google Scholar
27. Felix Heide, Steven Diamond, Matthias Nießner, Jonathan Ragan-Kelley, Wolfgang Heidrich, and Gordon Wetzstein. 2016. ProxImaL: Efficient image optimization using proximal algorithms. ACM Trans. Graph. 35, 4 (2016), 84:1–84:15.Google ScholarDigital Library
28. Nguyenho Ho, Sarah D. Olson, and Homer F. Walker. 2017. Accelerating the Uzawa algorithm. SIAM Journal on Scientific Computing 39, 5 (2017), S461–S476.Google ScholarCross Ref
29. Mingyi Hong, Zhi-Quan Luo, and Meisam Razaviyayn. 2016. Convergence analysis of alternating direction method of multipliers for a family of nonconvex problems. SIAM Journal on Optimization 26, 1 (2016), 337–364.Google ScholarCross Ref
30. Y. Hu, D. Zhang, J. Ye, X. Li, and X. He. 2013. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Transactions on Pattern Analysis and Machine Intelligence 35, 9 (2013), 2117–2130.Google ScholarDigital Library
31. Mojtaba Kadkhodaie, Konstantina Christakopoulou, Maziar Sanjabi, and Arindam Banerjee. 2015. Accelerated alternating direction method of multipliers (KDD ’15). 497–506.Google Scholar
32. Shahar Z. Kovalsky, Meirav Galun, and Yaron Lipman. 2016. Accelerated quadratic proxy for geometric optimization. ACM Trans. Graph. 35, 4 (2016), 134:1–134:11.Google ScholarDigital Library
33. Rongjie Lai and Stanley Osher. 2014. A splitting method for orthogonality constrained problems. Journal of Scientific Computing 58, 2 (2014), 431–449.Google ScholarDigital Library
34. Kenneth Lange. 2004. The MM Algorithm. In Optimization. Springer, 119–136.Google Scholar
35. Guoyin Li and Ting Kei Pong. 2015. Global convergence of splitting methods for nonconvex composite optimization. SIAM Journal on Optimization 25, 4 (2015), 2434–2460.Google ScholarCross Ref
36. Athanasios P Liavas and Nicholas D Sidiropoulos. 2015. Parallel algorithms for constrained tensor factorization via alternating direction method of multipliers. IEEE Transactions on Signal Processing 63, 20 (2015), 5450–5463.Google ScholarDigital Library
37. F. Lin, M. Fardad, and M. R. Jovanović. 2013. Design of optimal sparse feedback gains via the alternating direction method of multipliers. IEEE Trans. Automat. Control 58, 9 (2013), 2426–2431.Google ScholarCross Ref
38. T. Lin, S. Ma, and S. Zhang. 2015. On the global linear convergence of the ADMM with multiBlock variables. SIAM Journal on Optimization 25, 3 (2015), 1478–1497.Google ScholarCross Ref
39. K. Lipnikov, D. Svyatskiy, and Y. Vassilevski. 2013. Anderson acceleration for nonlinear finite volume scheme for advection-diffusion problems. SIAM Journal on Scientific Computing 35, 2 (2013), A1120–A1136.Google ScholarCross Ref
40. J. Liu, P. Musialski, P. Wonka, and J. Ye. 2013. Tensor completion for estimating missing values in visual data. IEEE Transactions on Pattern Analysis and Machine Intelligence 35, 1 (2013), 208–220.Google ScholarDigital Library
41. Ligang Liu, Lei Zhang, Yin Xu, Craig Gotsman, and Steven J. Gortler. 2008. A local/global approach to mesh parameterization. Computer Graphics Forum 27, 5 (2008), 1495–1504.Google ScholarDigital Library
42. Tiantian Liu, Adam W. Bargteil, James F. O’Brien, and Ladislav Kavan. 2013. Fast simulation of mass-spring systems. ACM Trans. Graph. 32, 6 (2013), 214:1–214:7.Google ScholarDigital Library
43. Tiantian Liu, Sofien Bouaziz, and Ladislav Kavan. 2017. Quasi-Newton methods for real-time simulation of hyperelastic materials. ACM Trans. Graph. 36, 3 (2017), 23:1–23:16.Google ScholarDigital Library
44. Yang Liu, Helmut Pottmann, Johannes Wallner, Yong-Liang Yang, and Wenping Wang. 2006. Geometric modeling with conical meshes and developable surfaces. ACM Trans. Graph. 25, 3 (2006), 681–689.Google ScholarDigital Library
45. Yang Liu, Weiwei Xu, Jun Wang, Lifeng Zhu, Baining Guo, Falai Chen, and Guoping Wang. 2011. General planar quadrilateral mesh design using conjugate direction field. ACM Trans. Graph. 30, 6 (2011), 140:1–140:10.Google ScholarDigital Library
46. Sindri Magnússon, Pradeep Chathuranga Weeraddana, Michael G Rabbat, and Carlo Fischione. 2016. On the convergence of alternating direction Lagrangian methods for nonconvex structured optimization problems. IEEE Transactions on Control of Network Systems 3, 3 (2016), 296–309.Google ScholarCross Ref
47. Sebastian Martin, Bernhard Thomaszewski, Eitan Grinspun, and Markus Gross. 2011. Example-based elastic materials. ACM Trans. Graph. 30, 4 (2011), 72:1–72:8.Google ScholarDigital Library
48. Ondrej Miksik, Vibhav Vineet, Patrick Pérez, and Phillip Torr. 2014. Distributed non-convex ADMM-based inference in large-scale random fields (BMVC 2014).Google Scholar
49. Yurii Nesterov. 1983. A method of solving a convex programming problem with convergence rate O(1/k2). Soviet Mathematics Doklady 27 (1983), 372–376.Google Scholar
50. Yurii Nesterov. 2013. Introductory Lectures on Convex Optimization: A Basic Course. Springer Science & Business Media.Google ScholarDigital Library
51. T. Neumann, K. Varanasi, C. Theobalt, M. Magnor, and M. Wacker. 2014. Compressed manifold modes for mesh processing. Computer Graphics Forum 33, 5 (2014), 35–44.Google ScholarDigital Library
52. Thomas Neumann, Kiran Varanasi, Stephan Wenger, Markus Wacker, Marcus Magnor, and Christian Theobalt. 2013. Sparse localized deformation components. ACM Trans. Graph. 32, 6 (2013), 179:1–179:10.Google ScholarDigital Library
53. Jorge Nocedal and Stephen J. Wright. 2006. Numerical Optimization (2nd ed.). Springer-Verlag New York.Google Scholar
54. M. Overby, G. E. Brown, J. Li, and R. Narain. 2017. ADMM ⊇ projective dynamics: Fast simulation of hyperelastic models with dynamic constraints. IEEE Transactions on Visualization and Computer Graphics 23, 10 (2017), 2222–2234.Google ScholarDigital Library
55. Zherong Pan and Dinesh Manocha. 2017. Efficient solver for spacetime control of smoke. ACM Trans. Graph. 36, 5 (2017).Google ScholarDigital Library
56. Yue Peng, Bailin Deng, Juyong Zhang, Fanyu Geng, Wenjie Qin, and Ligang Liu. 2018. Anderson acceleration for geometry optimization and physics simulation. ACM Trans. Graph. 37, 4 (2018), 42:1–42:14.Google ScholarDigital Library
57. Florian A. Potra and Hans Engler. 2013. A characterization of the behavior of the Anderson acceleration on linear problems. Linear Algebra Appl. 438, 3 (2013), 1002–1011.Google ScholarCross Ref
58. Phanisri P. Pratapa, Phanish Suryanarayana, and John E. Pask. 2016. Anderson acceleration of the Jacobi iterative method: An efficient alternative to Krylov methods for large, sparse linear systems. J. Comput. Phys. 306 (2016), 43–54.Google ScholarDigital Library
59. Péter Pulay. 1980. Convergence acceleration of iterative sequences. the case of SCF iteration. Chemical Physics Letters 73, 2 (1980), 393–398.Google ScholarCross Ref
60. P. Pulay. 1982. Improved SCF convergence acceleration. Journal of Computational Chemistry 3, 4 (1982), 556–560.Google ScholarCross Ref
61. Michael Rabinovich, Roi Poranne, Daniele Panozzo, and Olga Sorkine-Hornung. 2017. Scalable locally injective mappings. ACM Trans. Graph. 36, 2 (2017), 16:1–16:16.Google ScholarDigital Library
62. Ralph Tyrell Rockafellar. 1997. Convex Analysis. Princeton University Press.Google Scholar
63. R Tyrrell Rockafellar and Roger J-B Wets. 2009. Variational Analysis. Vol. 317. Springer Science & Business Media.Google Scholar
64. Thorsten Rohwedder and Reinhold Schneider. 2011. An analysis for the DIIS acceleration method used in quantum chemistry calculations. Journal of Mathematical Chemistry 49, 9 (2011), 1889–1914.Google ScholarCross Ref
65. Christian Schumacher, Bernhard Thomaszewski, Stelian Coros, Sebastian Martin, Robert Sumner, and Markus Gross. 2012. Efficient simulation of example-based materials (SCA ’12). 1–8.Google Scholar
66. W. Shi, Q. Ling, K. Yuan, G. Wu, and W. Yin. 2014. On the linear convergence of the ADMM in decentralized consensus optimization. IEEE Transactions on Signal Processing 62, 7 (2014), 1750–1761.Google ScholarDigital Library
67. Anna Shtengel, Roi Poranne, Olga Sorkine-Hornung, Shahar Z. Kovalsky, and Yaron Lipman. 2017. Geometric optimization via composite majorization. ACM Trans. Graph. 36, 4 (2017), 38:1–38:11.Google ScholarDigital Library
68. A. Simonetto and G. Leus. 2014. Distributed maximum likelihood sensor network localization. IEEE Transactions on Signal Processing 62, 6 (2014), 1424–1437.Google ScholarDigital Library
69. Olga Sorkine and Marc Alexa. 2007. As-rigid-as-possible surface modeling (SGP ’07). 109–116.Google Scholar
70. H. De Sterck. 2012. A nonlinear GMRES optimization algorithm for canonical tensor decomposition. SIAM Journal on Scientific Computing 34, 3 (2012), A1351–A1379.Google ScholarCross Ref
71. Phanish Suryanarayana, Phanisri P. Pratapa, and John E. Pask. 2019. Alternating Anderson-Richardson method: An efficient alternative to preconditioned Krylov methods for large, sparse linear systems. Computer Physics Communications 234 (2019), 278–285.Google ScholarCross Ref
72. J. Tao, J. Zhang, B. Deng, Z. Fang, Y. Peng, and Y. He. 2019. Parallel and scalable heat methods for geodesic distance computation. IEEE Transactions on Pattern Analysis and Machine Intelligence (2019).Google Scholar
73. Alex Toth, J. Austin Ellis, Tom Evans, Steven Hamilton, C. T. Kelley, Roger Pawlowski, and Stuart Slattery. 2017. Local improvement results for Anderson acceleration with inaccurate function evaluations. SIAM Journal on Scientific Computing 39, 5 (2017), S47–S65.Google ScholarCross Ref
74. Alex Toth and C. T. Kelley. 2015. Convergence analysis for Anderson acceleration. SIAM J. Numer. Anal. 53, 2 (2015), 805–819.Google ScholarCross Ref
75. Homer F. Walker and Peng Ni. 2011. Anderson acceleration for fixed-point iterations. SIAM J. Numer. Anal. 49, 4 (2011), 1715–1735.Google ScholarDigital Library
76. Congli Wang, Qiang Fu, Xiong Dun, and Wolfgang Heidrich. 2018. Megapixel adaptive optics: Towards correcting large-scale distortions in computational cameras. ACM Trans. Graph. 37, 4 (2018), 115:1–115:12.Google ScholarDigital Library
77. Huamin Wang. 2015. A Chebyshev semi-iterative approach for accelerating projective and position-based dynamics. ACM Trans. Graph. 34, 6 (2015), 246:1–246:9.Google ScholarDigital Library
78. Huamin Wang and Yin Yang. 2016. Descent methods for elastic body simulation on the GPU. ACM Trans. Graph. 35, 6 (2016), 212:1–212:10.Google ScholarDigital Library
79. Yu Wang, Wotao Yin, and Jinshan Zeng. 2019. Global convergence of ADMM in nonconvex nonsmooth optimization. Journal of Scientific Computing 78, 1 (2019), 29–63.Google ScholarDigital Library
80. Zaiwen Wen, Chao Yang, Xin Liu, and Stefano Marchesini. 2012. Alternating direction methods for classical and ptychographic phase retrieval. Inverse Problems 28, 11 (2012).Google Scholar
81. Chunlin Wu, Juyong Zhang, and Xue-Cheng Tai. 2011. Augmented Lagrangian method for total variation restoration with non-quadratic fidelity. Inverse Problems and Imaging 5, 1 (2011), 237–261.Google ScholarCross Ref
82. Jinhui Xiong, Ramzi Idoughi, Andres A. Aguirre-Pablo, Abdulrahman B. Aljedaani, Xiong Dun, Qiang Fu, Sigurdur T. Thoroddsen, and Wolfgang Heidrich. 2017. Rainbow particle imaging velocimetry for dense 3D fluid velocity imaging. ACM Trans. Graph. 36, 4 (2017), 36:1–36:14.Google ScholarDigital Library
83. Shiyao Xiong, Juyong Zhang, Jianmin Zheng, Jianfei Cai, and Ligang Liu. 2014. Robust surface reconstruction via dictionary learning. ACM Trans. Graph. 33, 6 (2014), 201:1–201:12.Google ScholarDigital Library
84. J. Yang, L. Luo, J. Qian, Y. Tai, F. Zhang, and Y. Xu. 2017. Nuclear norm based matrix regression with applications to face recognition with occlusion and illumination changes. IEEE Transactions on Pattern Analysis and Machine Intelligence 39, 1 (2017), 156–171.Google ScholarDigital Library
85. Juyong Zhang, Bailin Deng, Zishun Liu, Giuseppe Patanè, Sofien Bouaziz, Kai Hormann, and Ligang Liu. 2014. Local barycentric coordinates. ACM Trans. Graph. 33, 6 (2014), 188:1–188:12.Google ScholarDigital Library
86. Junzi Zhang, Brendan O’Donoghue, and Stephen Boyd. 2018. Globally convergent type-I Anderson acceleration for non-smooth fixed-point iterations. arXiv preprint arXiv:1808.03971 (2018).Google Scholar
87. Ruiliang Zhang and James T. Kwok. 2014. Asynchronous distributed ADMM for consensus optimization (ICML ’14). II-1701–II-1709.Google Scholar
88. Richard Y. Zhang and Jacob K. White. 2018. GMRES-accelerated ADMM for quadratic objectives. SIAM Journal on Optimization 28, 4 (2018), 3025–3056.Google ScholarCross Ref
89. Yufeng Zhu, Robert Bridson, and Danny M. Kaufman. 2018. Blended cured quasi-Newton for distortion optimization. ACM Trans. Graph. 37, 4 (2018), 40:1–40:14.Google ScholarDigital Library