“Crumpling sound synthesis” by Cirio, Li, Grinspun, Otaduy and Zheng
Conference:
Type(s):
Title:
- Crumpling sound synthesis
Session/Category Title: Sound & Pattern Synthesis
Presenter(s)/Author(s):
Abstract:
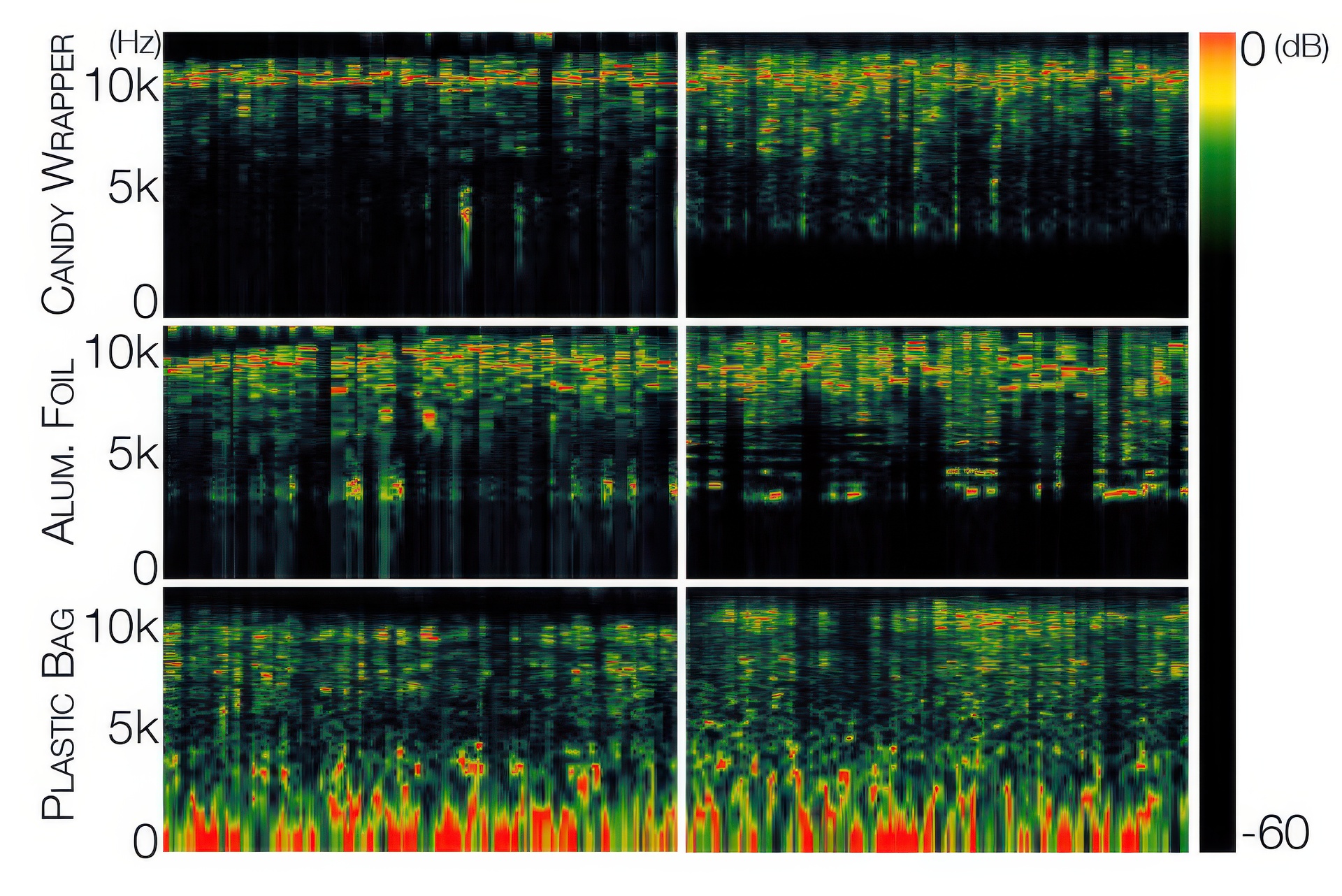
Crumpling a thin sheet produces a characteristic sound, comprised of distinct clicking sounds corresponding to buckling events. We propose a physically based algorithm that automatically synthesizes crumpling sounds for a given thin shell animation. The resulting sound is a superposition of individually synthesized clicking sounds corresponding to visually significant and insignificant buckling events. We identify visually significant buckling events on the dynamically evolving thin surface mesh, and instantiate visually insignificant buckling events via a stochastic model that seeks to mimic the power-law distribution of buckling energies observed in many materials.In either case, the synthesis of a buckling sound employs linear modal analysis of the deformed thin shell. Because different buckling events in general occur at different deformed configurations, the question arises whether the calculation of linear modes can be reused. We amortize the cost of the linear modal analysis by dynamically partitioning the mesh into nearly rigid pieces: the modal analysis of a rigidly moving piece is retained over time, and the modal analysis of the assembly is obtained via Component Mode Synthesis (CMS). We illustrate our approach through a series of examples and a perceptual user study, demonstrating the utility of the sound synthesis method in producing realistic sounds at practical computation times.
References:
1. Abobaker, M., Bouaziz, O., Lebyodkin, M., Lebedkina, T., and Shashkov, I. V. 2015. Avalanche dynamics in crumpled aluminum thin foils. Scripta Materialia 99 (Apr.), 17–20. Cross Ref
2. An, S. S., Marschner, S., and James, D. L. 2012. Motion-driven Concatenative Synthesis of Cloth Sounds. ACM Trans. Graph. 31, 4.
3. Balankin, A. S., Cruz, M. A. M., Caracheo, L. A. A., Huerta, O. S., Rivas, C. D., Martínez, C. L., Ochoa, D. S., Ruiz, L. M., Gutiérrez, S. M., Ortiz, J. P., and Ortiz, M. P. 2015. Mechanical properties and relaxation behavior of crumpled aluminum foils. Journal of Materials Science 50, 13. Cross Ref
4. Baraff, D., and Witkin, A. 1998. Large steps in cloth simulation. In Proc. SIGGRAPH ’98.
5. Bathe, K.-J., and Dong, J. 2014. Component mode synthesis with subspace iterations for controlled accuracy of frequency and mode shape solutions. Computers & Structures 139 (July).
6. Bridson, R., Marino, S., and Fedkiw, R. 2003. Simulation of clothing with folds and wrinkles. In Proc. SCA ’03.
7. Cerda, E., Chaieb, S., Melo, F., and Mahadevan, L. 1999. Conical dislocations in crumpling. Nature 401, 6748 (Sept.), 46–49. Cross Ref
8. Chadwick, J. N., An, S. S., and James, D. L. 2009. Harmonic shells: a practical nonlinear sound model for near-rigid thin shells. ACM Trans. Graph. 28, 5.
9. Choi, K.-J., and Ko, H.-S. 2002. Stable but Responsive Cloth. In Proc. SIGGRAPH ’02.
10. Cook, P. R. 2002. Real Sound Synthesis for Interactive Applications, 1st edition ed. A K Peters/CRC Press.
11. Craig, R. R., and Bampton, M. C. C. 1968. Coupling of substructures for dynamic analyses. AIAA Journal 6, 7, 1313–1319. Cross Ref
12. Craig, R. R., and Kurdila, A. J. 2006. Fundamentals of Structural Dynamics, 2 edition ed. Wiley, Hoboken, N.J, July.
13. Craig, J. R. 2000. Coupling of substructures for dynamic analyses: An overview. In 41st Structures, Structural Dynamics, and Materials Conference and Exhibit.
14. De Klerk, D., Rixen, D. J., and Voormeeren, S. N. 2008. General framework for dynamic substructuring. AIAA Journal 46, 5, 1169–1181. Cross Ref
15. DiDonna, B. A. 2002. Scaling of the buckling transition of ridges in thin sheets. Physical Review E 66, 1 (July), 016601. Cross Ref
16. Doel, K. v. d., Kry, P. G., and Pai, D. K. 2001. FoleyAutomatic: physically-based sound effects for interactive simulation and animation. In Proc. SIGGRAPH ’01.
17. Feller, W. 2008. An introduction to probability theory and its applications, vol. 2. John Wiley & Sons.
18. Fontana, F., and Bresin, R. 2003. Physics-based sound synthesis and control: Crushing, walking and running by crumpling sounds. In Proc. of the XIV Colloquium on Musical Informatics.
19. Gingold, Y., Secord, A., Han, J. Y., Grinspun, E., and Zorin, D. 2004. A Discrete Model for Inelastic Deformation of Thin Shells. Technical Report.
20. Golub, G. H., and Van Loan, C. F. 2012. Matrix computations, vol. 3. JHU Press.
21. Grinspun, E., Hirani, A. N., Desbrun, M., and Schröder, P. 2003. Discrete shells. In Proc. SCA ’03.
22. Holm-Jorgensen, K., and Nielsen, S. R. K. 2009. A component mode synthesis algorithm for multibody dynamics of wind turbines. Journal of Sound and Vibration 326, 753–767. Cross Ref
23. Houle, P. A., and Sethna, J. P. 1996. Acoustic Emission from crumpling paper. Physical Review E 54, 1 (July), 278–283. Cross Ref
24. Hurty, W. C. 1965. Dynamic Analysis of Structural Systems Using Component Modes. AIAA Journal 3, 4, 678–685. Cross Ref
25. James, D. L., and Twigg, C. D. 2005. Skinning mesh animations. ACM Trans. Graph. 24, 3.
26. James, D. L., Barbic, J., and Pai, D. K. 2006. Precomputed acoustic transfer: output-sensitive, accurate sound generation for geometrically complex vibration sources. ACM Trans. Graph. 25, 3.
27. Kim, T., Thürey, N., James, D. L., and Gross, M. H. 2008. Wavelet turbulence for fluid simulation. ACM Trans. Graph. 27, 3.
28. Kramer, E. M., and Lobkovsky, A. E. 1996. Universal Power Law in the Noise from a Crumpled Elastic Sheet. Physical Review E 53, 2 (Feb.), 1465–1469. Cross Ref
29. MacNeal, R. H. 1971. A hybrid method of component mode synthesis. Computers & Structures 1, 4 (Dec.), 581–601. Cross Ref
30. Moakher, M. 2002. Means and Averaging in the Group of Rotations. SIAM Journal on Matrix Analysis and Applications 24.
31. Narain, R., Samii, A., and O’Brien, J. F. 2012. Adaptive anisotropic remeshing for cloth simulation. ACM Trans. Graph. 31, 6.
32. Narain, R., Pfaff, T., and O’Brien, J. F. 2013. Folding and Crumpling Adaptive Sheets. ACM Trans. Graph. 32, 4.
33. O’Brien, J. F., Shen, C., and Gatchalian, C. M. Synthesizing sounds from rigid-body simulations. In Proc. SCA ’02.
34. O’Brien, J. F., Cook, P. R., and Essl, G. 2001. Synthesizing sounds from physically based motion. In Proc. SIGGRAPH ’01.
35. Pandey, A., Moulton, D. E., Vella, D., and Holmes, D. P. 2014. Dynamics of snapping beams and jumping poppers. EPL (Europhysics Letters) 105, 2, 24001. Cross Ref
36. Parlett, B. N. 1980. The symmetric eigenvalue problem, vol. 7. SIAM.
37. Petri, A., Paparo, G., Vespignani, A., Alippi, A., and Costantini, M. 1994. Experimental evidence for critical dynamics in microfracturing processes. Physical Review Letters 73, 25. Cross Ref
38. Ramm, E., and Wall, W. 2003. Shell Structures – a Sensitive Interrelation Between Physics and Numerics. Bericht. SFB 404.
39. Rubin, S. 1975. Improved Component-Mode Representation for Structural Dynamic Analysis. AIAA Journal 13, 8, 995–1006. Cross Ref
40. Rubinstein, R. Y., and Kroese, D. P. 2011. Simulation and the Monte Carlo method, vol. 707. John Wiley & Sons.
41. Schreck, C., Rohmer, D., James, D., Hahmann, S., and Cani, M.-P. 2016. Real-time sound synthesis for paper material based on geometric analysis. In Proc. SCA ’16.
42. Sethna, J. P., Dahmen, K. A., and Myers, C. R. 2001. Crackling noise. Nature 410, 6825 (Mar.), 242–250. Cross Ref
43. Shabana, A. A. 2012. Theory of vibration: Volume II: discrete and continuous systems. Springer Science & Business Media.
44. Shen, L., and Liu, Y. J. 2006. An adaptive fast multipole boundary element method for three-dimensional acoustic wave problems based on the Burton-Miller formulation. Computational Mechanics 40, 3 (Oct.), 461–472.
45. Stammberger, M., and Voss, H. 2008. Automated Multi-Level Substructuring for a Fluid-Solid Vibration Problem. In Numerical Mathematics and Advanced Applications. 563–570.
46. Sun, B. H., Yeh, K. Y., and Rimrott, F. P. J. 1995. On the buckling of structures. Technische Mechanik 15, 2, 129–140.
47. Terzopoulos, D., Platt, J., Barr, A., and Fleischer, K. 1987. Elastically deformable models. In Proc. SIGGRAPH ’87.
48. Vliegenthart, G. A., and Gompper, G. 2006. Forced crumpling of self-avoiding elastic sheets. Nature Materials 5, 3, 216–221. Cross Ref
49. Winnemöller, H., Olsen, S. C., and Gooch, B. 2006. Real-time video abstraction. ACM Trans. Graph. 25, 3.
50. Wood, A. 2002. Witten’s lectures on crumpling. Physica A: Statistical Mechanics and its Applications 313, 1.
51. Yang, Y., Xu, W., Guo, X., Zhou, K., and Guo, B. 2013. Boundary-Aware Multidomain Subspace Deformation. IEEE TVCG 19, 10.
52. Zheng, C., and James, D. L. 2010. Rigid-body fracture sound with precomputed soundbanks. ACM Trans. Graph. 29, 4.
53. Zheng, C., and James, D. L. 2011. Toward high-quality modal contact sound. ACM Trans. Graph. 30, 4.
54. Zhou, C., Jin, X., and Wang, C. C. L. 2008. Shear buckling and dynamic bending in cloth simulation. Computer Animation and Virtual Worlds 19, 3-4 (Jan.), 493–503.