“Decoupling simulation accuracy from mesh quality”
Conference:
Type(s):
Title:
- Decoupling simulation accuracy from mesh quality
Session/Category Title: Structured simulation
Presenter(s)/Author(s):
Moderator(s):
Abstract:
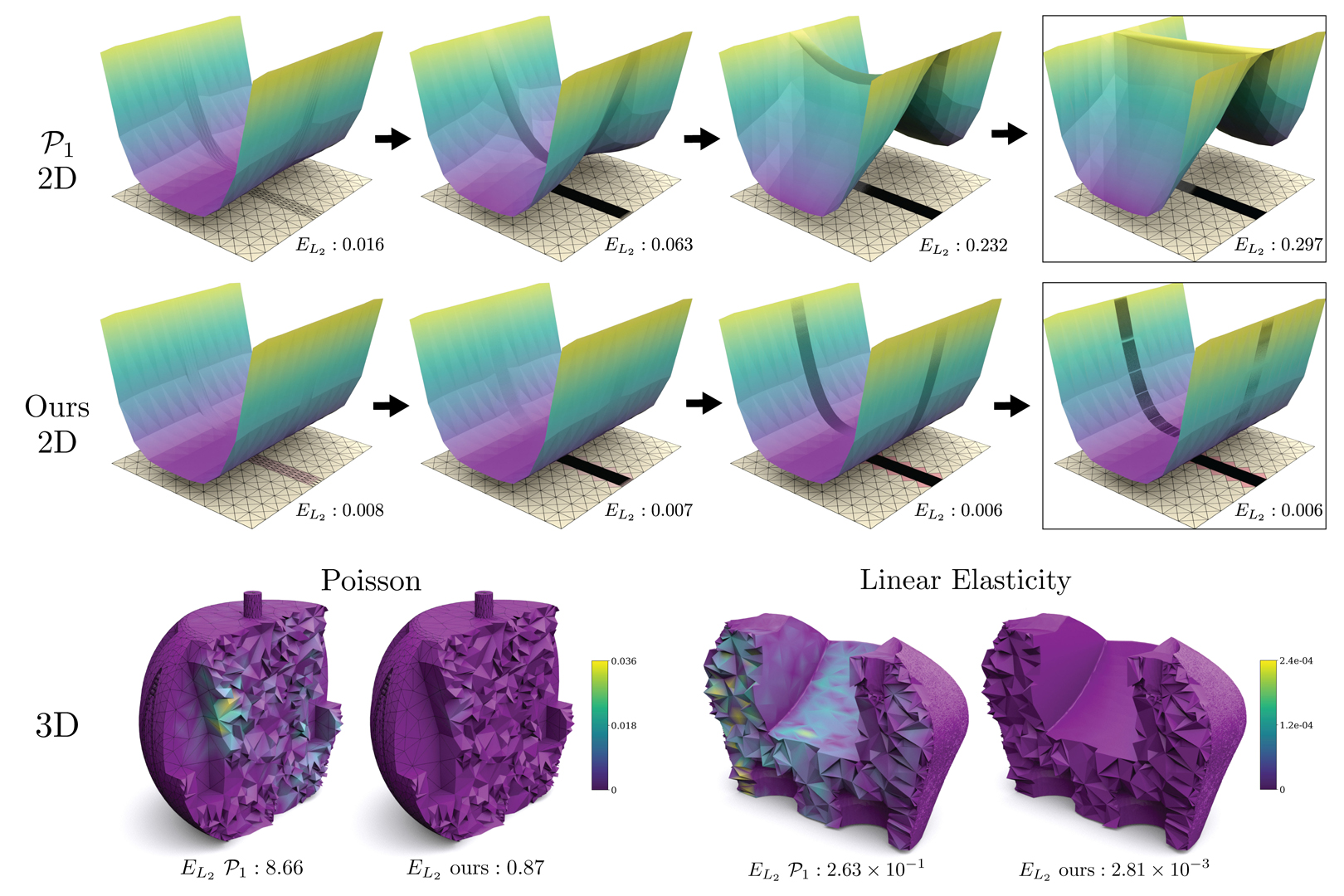
For a given PDE problem, three main factors affect the accuracy of FEM solutions: basis order, mesh resolution, and mesh element quality. The first two factors are easy to control, while controlling element shape quality is a challenge, with fundamental limitations on what can be achieved.We propose to use p-refinement (increasing element degree) to decouple the approximation error of the finite element method from the domain mesh quality for elliptic PDEs.Our technique produces an accurate solution even on meshes with badly shaped elements, with a slightly higher running time due to the higher cost of high-order elements. We demonstrate that it is able to automatically adapt the basis to badly shaped elements, ensuring an error consistent with high-quality meshing, without any per-mesh parameter tuning. Our construction reduces to traditional fixed-degree FEM methods on high-quality meshes with identical performance.Our construction decreases the burden on meshing algorithms, reducing the need for often expensive mesh optimization and automatically compensates for badly shaped elements, which are present due to boundary constraints or limitations of current meshing methods. By tackling mesh generation and finite element simulation jointly, we obtain a pipeline that is both more efficient and more robust than combinations of existing state of the art meshing and FEM algorithms.
References:
1. B. Aksoylu, A. Khodakovsky, and P. Schröder. 2005. Multilevel Solvers for Unstructured Surface Meshes. SIAM J. Sri. Comput. 26, 4 (April 2005), 1146–1165. Google ScholarDigital Library
2. G. Alzetta, D. Arndt, W. Bangerth, V. Boddu, B. Brands, D. Davydov, R. Gassmoeller, T. Heister, L. Heltai, K. Kormann, M. Kronbichler, M. Maier, J.-P. Pelteret, B. Turcksin, and D. Wells. 2018. The deal. II Library, Version 9.0. Journal of Numerical Mathematics (2018).Google Scholar
3. I. Babuska, A. Craig, J. Mandel, and J. Pitkaranta. 1991. Efficient Preconditioning for the p-Version Finite Element Method in Two Dimensions. SIAM J. Numer. Anal. 28, 3(1991), 624–661. Google ScholarDigital Library
4. I. Babuška and M. Suri. 1994. The p and h-p versions of the finite element method, basic principles and properties. SIAM review 36, 4 (1994), 578–632. Google ScholarDigital Library
5. W. Bangerth, R. Hartmann, and G. Kanschat. 2007. deal. II – a general-purpose object-oriented finite element library. ACM Transactions on Mathematical Software (TOMS) 33, 4 (2007), 24. Google ScholarDigital Library
6. A. W. Bargteil and E. Cohen. 2014. Animation of deformable bodies with quadratic Bézier finite elements. ACM Transactions on Graphics (TOG) 33, 3 (2014), 27. Google ScholarDigital Library
7. D. Bommes, B. Levy, N. Pietroni, E. Puppo, C. Silva, M. Tarini, and D. Zorin. 2012. State of the Art in Quad Meshing. In Eurographics STARS. Cagliari, Italy.Google Scholar
8. M. Botsch, M. Pauly, M. Gross, and L. Kobbelt. 2006. PriMo: Coupled Prisms for Intuitive Surface Modeling. In Proceedings of the Fourth Eurographics Symposium on Geometry Processing (SGP ’06). Eurographics Association, 11–20. Google ScholarDigital Library
9. D. Braess. 2007. Finite elements: Theory, fast solvers, and applications in solid mechanics. Cambridge University Press.Google Scholar
10. P. G. Ciarlet. 1976. Numerical analysis of the finite element method. Vol. 59. Presses de l’Université de Montreal.Google Scholar
11. P. G. Ciarlet and P. Raviart. 1972. General Lagrange and Hermite interpolation in Rn with applications to finite element methods. Archive for Rational Mechanics and Analysis 46, 3 (1972), 177–199.Google ScholarCross Ref
12. A. De Coninck, B. De Baets, D. Kourounis, F. Verbosio, O. Schenk, S. Maenhout, and J. Fostier. 2016. Needles: Toward Large-Scale Genomic Prediction with Marker-by-Environment Interaction. 203, 1 (2016), 543–555.Google Scholar
13. C. Dobrzynski. 2012. MMG3D: user guide.Google Scholar
14. A. Düster, S. Hartmann, and E. Rank. 2003. p-FEM applied to finite isotropic hyperelastic bodies. Computer Methods in Applied Mechanics and Engineering 192, 47–48 (2003), 5147–5166.Google ScholarCross Ref
15. E. Edwards and R. Bridson. 2014. Detailed water with coarse grids: combining surface meshes and adaptive discontinuous Galerkin. ACM Transactions on Graphics (TOG) 33, 4 (2014), 136. Google ScholarDigital Library
16. R. D. Falgout and U. M. Yang. 2002. hypre: A Library of High Performance Preconditioners. In Computational Science — ICCS 2002, Peter M. A. Sloot, Alfons G. Hoekstra, C. J. Kenneth Tan, and Jack J. Dongarra (Eds.). Springer Berlin Heidelberg, Berlin, Heidelberg, 632–641. Google ScholarDigital Library
17. D. Franke, A. Düster, and E. Rank. 2008. The p-version of the FEM for computational contact mechanics. PAMM 8, 1 (2008), 10271–10272.Google ScholarCross Ref
18. R. Franke. 1979. A Critical Comparison of Some Methods for Interpolation of Scattered Data.Google Scholar
19. E. Grinspun, P. Krysl, and P. Schröder. 2002. CHARMS: a simple framework for adaptive simulation. ACM transactions on graphics (TOG) 21, 3 (2002), 281–290. Google ScholarDigital Library
20. G. Guennebaud, B.Jacob, et al. 2010. Eigen v3.Google Scholar
21. K. Hormann, K. Polthier, and A. Sheffer. 2008. Mesh Parameterization: Theory and Practice. In ACM SIGGRAPH ASIA 2008 Courses (SIGGRAPH Asia ’08). ACM, New York, NY, USA, Article 12, 87 pages. Google ScholarDigital Library
22. Y. Hu, Q. Zhou, X. Gao, A. Jacobson, D. Zorin, and D. Panozzo. 2018. Tetrahedral Meshing in the Wild. ACM Trans. Graph. 37, 4, Article 60 (July 2018), 14 pages. Google ScholarDigital Library
23. A. Jacobson, I. Baran, J. Popovic, and O. Sorkine. 2011. Bounded biharmonic weights for real-time deformation. ACM Trans. Graph. 30, 4 (2011), 78-1. Google ScholarDigital Library
24. W. Jakob, M. Tarini, D. Panozzo, and O. Sorkine-Hornung. 2015. Instant Field-Aligned Meshes. ACM Transactions on Graphics (Proceedings of SIGGRAPH ASIA) 34, 6 (Nov. 2015). Google ScholarDigital Library
25. C. Jamin, P. Alliez, M. Yvinec, and J.-D. Boissonnat. 2015. CGALmesh: a generic framework for delaunay mesh generation. ACM Transactions on Mathematical Software (TOMS) 41, 4 (2015), 23. Google ScholarDigital Library
26. P. Kaufmann, O. Wang, A. Sorkine-Hornung, O. Sorkine-Hornung, A. Smolic, and M. Gross. 2013. Finite Element Image Warping. Computer Graphics Forum (proceedings of EUROGRAPHICS) 32, 2 (2013), 31–39.Google Scholar
27. M. Kazhdan and H. Hoppe. 2013. Screened Poisson Surface Reconstruction. ACM Trans. Graph. 32, 3, Article 29 (July 2013), 13 pages. Google ScholarDigital Library
28. M. Kim, G. Pons-Moll, S. Pujades, S. Bang, J. Kim, M. Black, and S.-H. Lee. 2017. Data-Driven Physics for Human Soft Tissue Animation. ACM Transactions on Graphics, (Proc. SIGGRAPH) 36, 4 (2017). Google ScholarDigital Library
29. K. Kobayashi and T. Tsuchiya. 2016. Error analysis of Lagrange interpolation on tetrahedrons. arXiv preprint arXiv.1606.03918 (2016).Google Scholar
30. D. Kourounis, A. Fuchs, and O. Schenk. 2018. Towards the Next Generation of Multiperiod Optimal Power Flow Solvers. IEEE Transactions on Power Systems PP, 99 (2018), 1–10.Google Scholar
31. R. Ling, J. Huang, B. Jüttler, F. Sun, H. Bao, and W. Wang. 2014. Spectral quadrangulation with feature curve alignment and element size control. ACM Transactions on Graphics (TOG) 34, 1 (2014), 11. Google ScholarDigital Library
32. T. Liu, S. Bouaziz, and L. Kavan. 2017. Quasi-Newton methods for real-time simulation of hyperelastic materials. ACM Transactions on Graphics (TOG) 36, 3 (2017), 23. Google ScholarDigital Library
33. P.-L. Manteaux, C. Wojtan, R. Narain, S. Redon, F. Faure, and M.-P. Cani. 2017. Adaptive physically based models in computer graphics. In Computer Graphics Forum, Vol. 36. Wiley Online Library, 312–337. Google ScholarDigital Library
34. A. McAdams, Y. Zhu, A. Selle, M. Empey, R. Tamstorf, J. Teran, and E. Sifakis. 2011. Efficient Elasticity for Character Skinning with Contact and Collisions. In ACM SIGGRAPH 2011 Papers (SIGGRAPH ’11). ACM, New York, NY, USA, Article 37, 12 pages. Google ScholarDigital Library
35. W. F. Mitchell. 2013. A Collection of 2D Elliptic Problems for Testing Adaptive Grid Refinement Algorithms. Appl. Math. Comput. 220 (Sept. 2013), 350–364. Google ScholarDigital Library
36. W. F. Mitchell and M. A. McClain. 2014. A comparison of hp-adaptive strategies for elliptic partial differential equations. ACM Transactions on Mathematical Software (TOMS) 41, 1 (2014), 2. Google ScholarDigital Library
37. P. Musialski, C. Hafner, F. Rist, M. Birsak, M. Wimmer, and L. Kobbelt. 2016. Non-linear shape optimization using local subspace projections. ACM Transactions on Graphics (TOG) 35, 4 (2016), 87. Google ScholarDigital Library
38. M. Ong. 1994. Uniform Refinement of a Tetrahedron. SIAM Journal on Scientific Computing 15, 5 (1994), 1134–1144. Google ScholarDigital Library
39. A. Orzan, A. Bousseau, H. Winnemöller, P. Barla, J. Thollot, and D. Salesin. 2008. Diffusion Curves: A Vector Representation for Smooth-Shaded Images. In ACM Transactions on Graphics (Proceedings of SIGGRAPH 2008), Vol. 27. Google ScholarDigital Library
40. J. Panetta, Q. Zhou, L. Malomo, N. Pietroni, P. Cignoni, and D. Zorin. 2015. Elastic textures for additive fabrication. ACM Transactions on Graphics (TOG) 34, 4 (2015), 135. Google ScholarDigital Library
41. T. Pfaff, R. Narain, J. M. De Joya, and J. F. O’Brien. 2014. Adaptive tearing and cracking of thin sheets. ACM Transactions on Graphics (TOG) 33, 4 (2014), 110. Google ScholarDigital Library
42. U. Pinkall and K. Polthier. 1993. Computing Discrete Minimal Surfaces and Their Conjugates. Experimental Mathematics 2 (1993), 15–36.Google ScholarCross Ref
43. M. Piovarči, D. I. Levin, J. Rebello, D. Chen, R. Ďurikovič, H. Pfister, W. Matusik, and P. Didyk. 2016. An interaction-aware, perceptual model for non-linear elastic objects. ACM Transactions on Graphics (TOG) 35, 4 (2016), 55. Google ScholarDigital Library
44. C. Schwab. 1998. p-and hp-finite element methods: Theory and applications in solid and fluid mechanics. Oxford University Press.Google Scholar
45. M. Seiler, D. Steinemann, J. Spillmann, and M. Harders. 2011. Robust interactive cutting based on an adaptive octree simulation mesh. The Visual Computer 27, 6–8 (2011), 519–529. Google ScholarDigital Library
46. J. Shewchuk. 2002. What is a good linear finite element? interpolation, conditioning, anisotropy, and quality measures (preprint). University of California at Berkeley 73 (2002), 137.Google Scholar
47. J. R. Shewchuk. 1996. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. In Applied computational geometry towards geometric engineering. Springer, 203–222. Google ScholarDigital Library
48. L. Shi, Y. Yu, N. Bell, and W.-W. Feng. 2006. A Fast Multigrid Algorithm for Mesh Deformation. ACM Trans. Graph. 25, 3 (July 2006), 1108–1117. Google ScholarDigital Library
49. H. Si. 2015. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Transactions on Mathematical Software (TOMS) 41, 2 (2015), 11. Google ScholarDigital Library
50. T. J. Simnett, S. D. Laycock, and A. M. Day. 2009. An Edge-based Approach to Adaptively Refining a Mesh for Cloth Deformation.. In TPCG. 77–84.Google Scholar
51. O. Sorkine. 2005. Laplacian Mesh Processing. In Eurographics 2005 – State of the Art Reports, Yiorgos Chrysanthou and Marcus Magnor (Eds.). The Eurographics Association.Google Scholar
52. A. Stuart, J. Levine, B. Jones, and A. Bargteil. 2013. Automatic Construction of Coarse, High-Quality Tetrahedralizations that Enclose and Approximate Surfaces for Animation. In Proceedings of the ACM SIGGRAPH Conference on Motion in Games. Google ScholarDigital Library
53. K. Takayama, O. Sorkine, A. Nealen, and T. Igarashi. 2010. Volumetric modeling with diffusion surfaces. In ACM Transactions on Graphics (TOG), Vol. 29. ACM, 180. Google ScholarDigital Library
54. D. Terzopoulos, J. Platt, A. Barr, and K. Fleischer. 1987. Elastically deformable models. ACM Siggraph Computer Graphics 21, 4 (1987), 205–214. Google ScholarDigital Library
55. A. Vaxman, M. Campen, O. Diamanti, D. Bommes, K. Hildebrandt, M. Ben-Chen, and D. Panozzo. 2016. Directional Field Synthesis, Design, and Processing. In SIGGRAPH ASIA 2016 Courses (SA ’16). ACM, New York, NY, USA, Article 15, 30 pages. Google ScholarDigital Library
56. F. Verbosio, A. D. Coninck, D. Kourounis, and O. Schenk. 2017. Enhancing the scalability of selected inversion factorization algorithms in genomic prediction. Journal of Computational Science 22, Supplement C (2017), 99–108.Google Scholar
57. J.-H. Wang, R. Setaluri, D. L. James, and D. K. Pai. 2017. Bounce maps: an improved restitution model for real-time rigid-body impact. ACM Transactions on Graphics (TOG) 36, 4 (2017), 150. Google ScholarDigital Library
58. Y. Wang, A. Jacobson, J. Barbič, and L. Kavan. 2015. Linear subspace design for real-time shape deformation. ACM Transactions on Graphics (TOG) 34, 4 (2015), 57. Google ScholarDigital Library
59. M. Wicke, D. Ritchie, B. M. Klingner, S. Burke, J. R. Shewchuk, and J. F. O’Brien. 2010. Dynamic local remeshing for elastoplastic simulation. In ACM Transactions on graphics (TOG), Vol. 29. ACM, 49. Google ScholarDigital Library
60. C. Wojtan and G. Turk. 2008. Fast viscoelastic behavior with thin features. ACM transactions on graphics (TOG) 27, 3 (2008), 47. Google ScholarDigital Library
61. X. Wu, M. S. Downes, T. Goktekin, and F. Tendick. 2001. Adaptive nonlinear finite elements for deformable body simulation using dynamic progressive meshes. In Computer Graphics Forum, Vol. 20. Wiley Online Library, 349–358.Google Scholar
62. H. Xiao and Z. Gimbutas. 2010. A numerical algorithm for the construction of efficient quadrature rules in two and higher dimensions. Computers & Mathematics with Applications 59, 2 (2010), 663–676. Google ScholarCross Ref
63. H. Xu and J. Barbič. 2016. Pose-Space Subspace Dynamics. ACM Trans. on Graphics (SIGGRAPH 2016) 35, 4 (2016). Google ScholarDigital Library
64. Q. Zhou and A. Jacobson. 2016. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv preprint arXiv: 1605.04797 (2016).Google Scholar
65. Q. Zhou, J. Panetta, and D. Zorin. 2013. Worst-case structural analysis. ACM Trans. Graph. 32, 4 (2013), 137–1. Google ScholarDigital Library
66. B. Zhu, M. Skouras, D. Chen, and W. Matusik. 2017. Two-Scale Topology Optimization with Microstructures. ACM Trans. Graph. 36, 4, Article 120b (July 2017).Google ScholarDigital Library
67. Y Zhu, E. Sifakis, J. Teran, and A. Brandt. 2010. An Efficient Multigrid Method for the Simulation of High-resolution Elastic Solids. ACM Trans. Graph. 29, 2, Article 16 (April 2010), 18 pages. Google ScholarDigital Library