“Multiscale vector volumes”
Conference:
Type(s):
Title:
- Multiscale vector volumes
Session/Category Title: Shape & Vector Representations
Presenter(s)/Author(s):
Abstract:
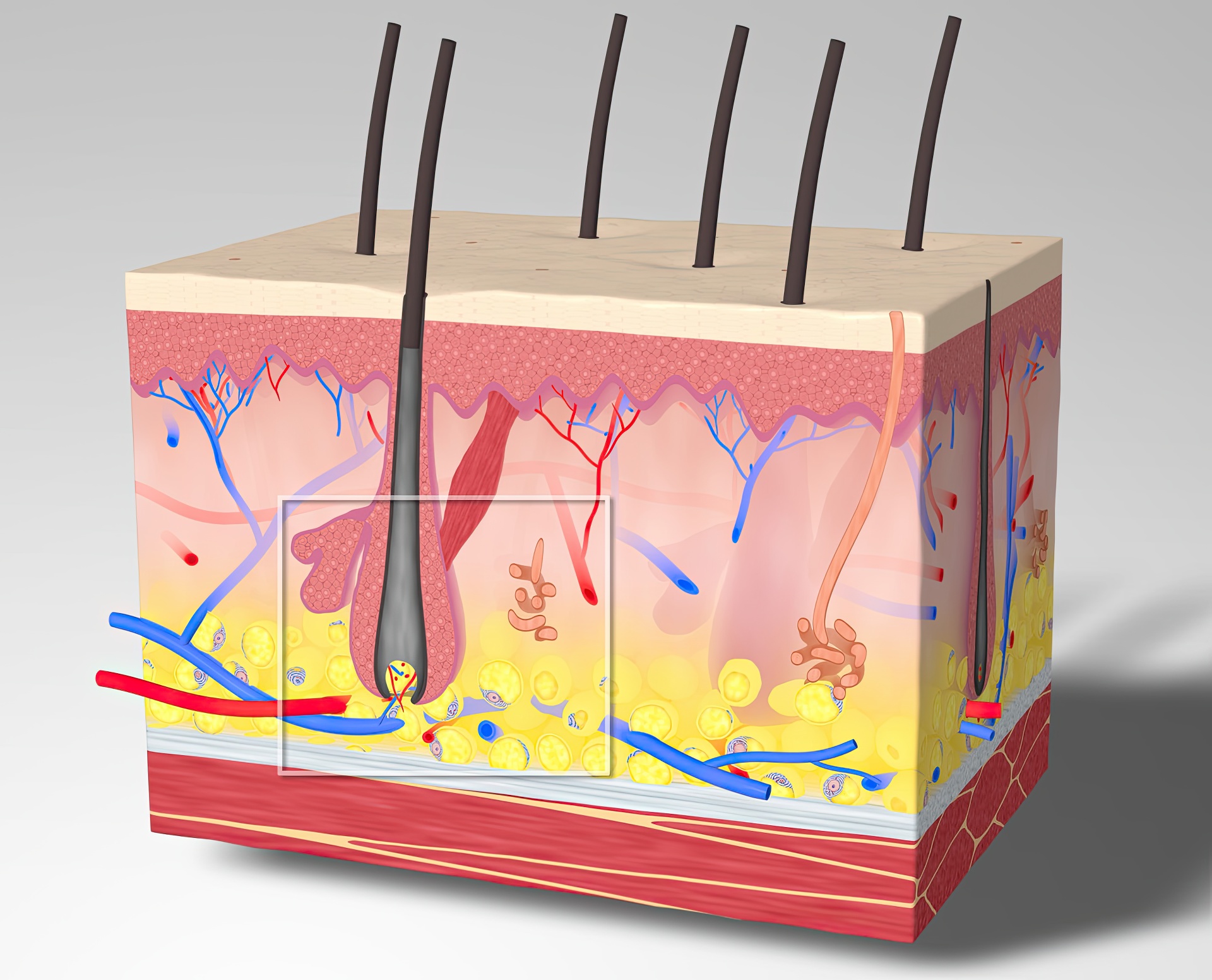
We introduce multiscale vector volumes, a compact vector representation for volumetric objects with complex internal structures spanning a wide range of scales. With our representation, an object is decomposed into components and each component is modeled as an SDF tree, a novel data structure that uses multiple signed distance functions (SDFs) to further decompose the volumetric component into regions. Multiple signed distance functions collectively can represent non-manifold surfaces and deliver a powerful vector representation for complex volumetric features. We use multiscale embedding to combine object components at different scales into one complex volumetric object. As a result, regions with dramatically different scales and complexities can co-exist in an object. To facilitate volumetric object authoring and editing, we have also developed a scripting language and a GUI prototype. With the help of a recursively defined spatial indexing structure, our vector representation supports fast random access, and arbitrary cross sections of complex volumetric objects can be visualized in real time.
References:
1. Corcoran, A. L., and Wainwright, R. L. 1992. A genetic algorithm for packing in three dimensions. In Proceedings of ACM/SIGAPP Symposium on Applied Computing, 1021–1030. Google ScholarDigital Library
2. Cutler, B., Dorsey, J., McMillan, L., Müller, M., and Jagnow, R. 2002. A procedural approach to authoring solid models. ACM Trans. Graph. 21, 3, 302–311. Google ScholarDigital Library
3. Dong, Y., Lefebvre, S., Tong, X., and Drettakis, G. 2008. Lazy solid texture synthesis. Computer Graphics Forum 27, 4, 1165–1174. Google ScholarDigital Library
4. Frisken, S. F., Perry, R. N., Rockwood, A. P., and Jones, T. R. 2000. Adaptively sampled distance fields: a general representation of shape for computer graphics. In Proceedings of SIGGRAPH 2000, 249–254. Google ScholarDigital Library
5. Hable, J., and Rossignac, J. 2005. Blister: GPU-based rendering of Boolean combinations of free-form triangulated shapes. ACM Trans. Graph. 24, 3, 1024–1031. Google ScholarDigital Library
6. Hadwiger, M., Sigg, C., Scharsach, H., Bühler, K., and Gross, M. 2005. Real-time ray-casting and advanced shading of discrete isosurfaces. Computer Graphics Forum 24, 3, 303–312.Google ScholarCross Ref
7. Han, C., Risser, E., Ramamoorthi, R., and Grinspun, E. 2008. Multiscale texture synthesis. ACM Trans. Graph. 27, 3, 51:1–51:8. Google ScholarDigital Library
8. Jones, M. W. 1995. 3D distance from a point to a triangle. Tech. Rep. CSR-5-95, University of Wales Swansea.Google Scholar
9. Kopf, J., Fu, C.-W., Cohen-Or, D., Deussen, O., Lischinski, D., and Wong, T.-T. 2007. Solid texture synthesis from 2D exemplars. ACM Trans. Graph. 26, 3, 2:1–2:9. Google ScholarDigital Library
10. Perlin, K., and Hoffert, E. M. 1989. Hypertexture. In Proceedings of SIGGRAPH ’89, 253–262. Google ScholarDigital Library
11. Perry, R. N., and Frisken, S. F. 2006. Method for generating a two-dimensional distance field within a cell associated with a corner of a two-dimensional object. US Patent No. US 7,034,830.Google Scholar
12. Ricci, A. 1974. A constructive geometry for computer graphics. Computer Journal 16, 2, 157–160.Google ScholarCross Ref
13. Shishkovtsov, O. 2005. Deferred shading in S. T.A.L.K.E.R. In GPU Gems 2. ch. 9, 143–166.Google Scholar
14. Sigg, C., and Hadwiger, M. 2005. Fast third-order texture filtering. In GPU Gems 2. ch. 20, 313–329.Google Scholar
15. Takayama, K., Okabe, M., Ijiri, T., and Igarashi, T. 2008. Lapped solid textures: filling a model with anisotropic textures. ACM Trans. Graph. 27, 5, 53:1–53:9. Google ScholarDigital Library
16. Takayama, K., Sorkine, O., Nealen, A., and Igarashi, T. 2010. Volumetric modeling with diffusion surfaces. ACM Trans. Graph. 29, 5, 180:1–180:8. Google ScholarDigital Library
17. Wang, L., Zhou, K., Yu, Y., and Guo, B. 2010. Vector solid textures. ACM Trans. Graph. 29, 4, 86:1–86:8. Google ScholarDigital Library
18. Wei, L.-Y. 2008. Parallel Poisson disk sampling. ACM Trans. Graph. 27, 3, 20:1–20:9. Google ScholarDigital Library