“Joint shape segmentation with linear programming”
Conference:
Type(s):
Title:
- Joint shape segmentation with linear programming
Session/Category Title: Shape Analysis and Deformation
Presenter(s)/Author(s):
Abstract:
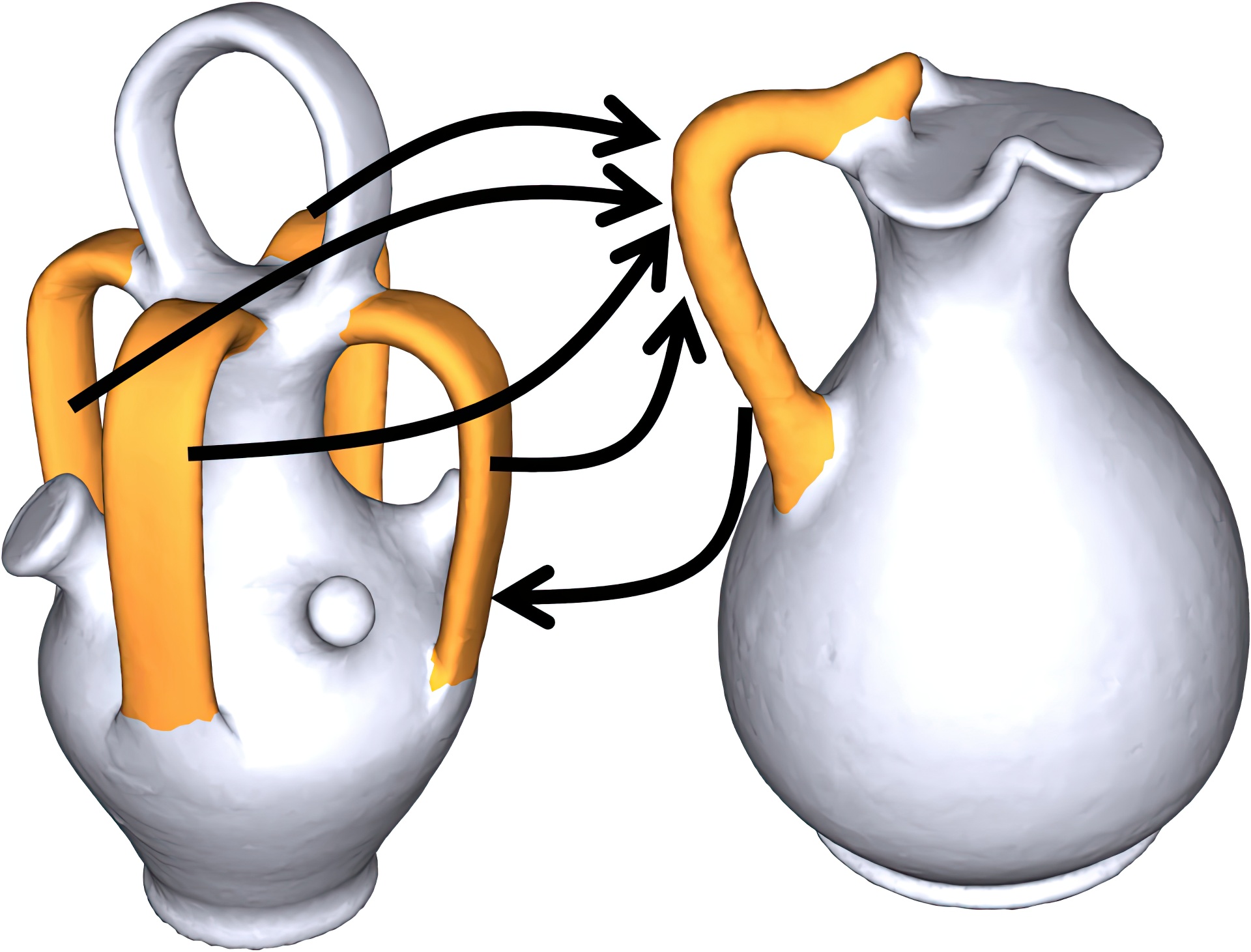
We present an approach to segmenting shapes in a heterogenous shape database. Our approach segments the shapes jointly, utilizing features from multiple shapes to improve the segmentation of each. The approach is entirely unsupervised and is based on an integer quadratic programming formulation of the joint segmentation problem. The program optimizes over possible segmentations of individual shapes as well as over possible correspondences between segments from multiple shapes. The integer quadratic program is solved via a linear programming relaxation, using a block coordinate descent procedure that makes the optimization feasible for large databases. We evaluate the presented approach on the Princeton segmentation benchmark and show that joint shape segmentation significantly outperforms single-shape segmentation techniques.
References:
1. Anguelov, D., Srinivasan, P., Pang, H., Koller, D., Thrun, S., and Davis, J. 2005. The correlated correspondence algorithm for unsupervised registration of nonrigid surfaces. In Proc. Neural Information Processing Systems (NIPS), The MIT Press.Google Scholar
2. Boyd, S., and Vandenberghe, L. 2004. Convex Optimization. Cambridge University Press. Google ScholarDigital Library
3. Chang, W., and Zwicker, M. 2008. Automatic registration for articulated shapes. In Proc. Symposium on Geometry Processing, Eurographics Association. Google ScholarDigital Library
4. Chaudhuri, S., Kalogerakis, E., Guibas, L., and Koltun, V. 2011. Probabilistic reasoning for assembly-based 3d modeling. In Proc. SIGGRAPH, ACM. Google ScholarDigital Library
5. Chen, X., Golovinskiy, A., and Funkhouser, T. 2009. A benchmark for 3d mesh segmentation. In Proc. SIGGRAPH, ACM. Google ScholarDigital Library
6. Golovinskiy, A., and Funkhouser, T. 2008. Randomized cuts for 3d mesh analysis. In Proc. SIGGRAPH Asia, ACM. Google ScholarDigital Library
7. Golovinskiy, A., and Funkhouser, T. 2009. Consistent segmentation of 3d models. Computers & Graphics 33, 3, 262–269. Google ScholarDigital Library
8. Grant, M., and Boyd, S. 2011. CVX: Matlab Software for Disciplined Convex Programming. http://www.stanford.edu/~boyd/cvx/.Google Scholar
9. Kalogerakis, E., Hertzmann, A., and Singh, K. 2010. Learning 3d mesh segmentation and labeling. In Proc. SIGGRAPH, ACM. Google ScholarDigital Library
10. Katz, S., and Tal, A. 2003. Hierarchical mesh decomposition using fuzzy clustering and cuts. In Proc. SIGGRAPH, ACM. Google ScholarDigital Library
11. Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. 2004. Shape matching and anisotropy. In Proc. SIGGRAPH, ACM. Google ScholarDigital Library
12. Kraevoy, V., Julius, D., and Sheffer, A. 2007. Model composition from interchangeable components. In Proc. Pacific Graphics, IEEE Computer Society, 129–138. Google ScholarDigital Library
13. Kumar, M. P., Kolmogorov, V., and Torr, P. H. S. 2009. An analysis of convex relaxations for MAP estimation of discrete MRFs. Journal of Machine Learning Research 10, 71–106. Google ScholarDigital Library
14. Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D. 2002. Shape distributions. ACM Transactions on Graphics 21, 4, 807–832. Google ScholarDigital Library
15. Rand, W. M. 1971. Objective criteria for the evaluation of clustering methods. Journal of the American Statistical Association 66, 846–850.Google ScholarCross Ref
16. Ren, X., and Malik, J. 2003. Learning a classification model for segmentation. In Proc. IEEE International Conference on Computer Vision. Google ScholarDigital Library
17. Shamir, A. 2008. A survey on mesh segmentation techniques. Computer Graphics Forum 27, 1539–1556.Google ScholarCross Ref
18. Shapira, L., Shamir, A., and Cohen-Or, D. 2008. Consistent mesh partitioning and skeletonisation using the shape diameter function. The Visual Computer 24, 4, 249–259. Google ScholarDigital Library
19. Shapira, L., Shalom, S., Shamir, A., Cohen-Or, D., and Zhang, H. 2010. Contextual part analogies in 3d objects. International Journal of Computer Vision 89, 309–326. Google ScholarDigital Library
20. Shi, J., and Malik, J. 2000. Normalized cuts and image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 22, 8, 888–905. Google ScholarDigital Library
21. Shotton, J., Winn, J., Rother, C., and Criminisi, A. 2009. Textonboost for image understanding: multi-class object recognition and segmentation by jointly modeling texture, layout, and context. International Journal of Computer Vision 81, 2–23. Google ScholarDigital Library
22. Sidi, O., van Kaick, O., Kleiman, Y., Zhang, H., and Cohen-Or, D. 2011. Unsupervised co-segmentation of a set of shapes via descriptor-space spectral clustering. ACM Trans. Graph. 30 (December), 126:1–126:9. Google ScholarDigital Library
23. Simari, P., Nowrouzezahrai, D., Kalogerakis, E., and Singh, K. 2009. Multi-objective shape segmentation and labeling. Computer Graphics Forum 28, 5, 1415–1425. Google ScholarDigital Library
24. Sontag, D., and Jaakkola, T. 2009. Tree block coordinate descent for MAP in graphical models. Journal of Machine Learning Research – Proceedings Track 5, 544–551.Google Scholar
25. Wainwright, M. J., Jaakkola, T., and Willsky, A. S. 2005. MAP estimation via agreement on trees: message-passing and linear programming. IEEE Transactions on Information Theory 51, 11, 3697–3717. Google ScholarDigital Library
26. Xu, K., Li, H., Zhang, H., Cohen-Or, D., Xiong, Y., and Cheng, Z.-Q. 2010. Style-content separation by anisotropic part scales. ACM Trans. Graph. 29 (December), 184:1–184:10. Google ScholarDigital Library