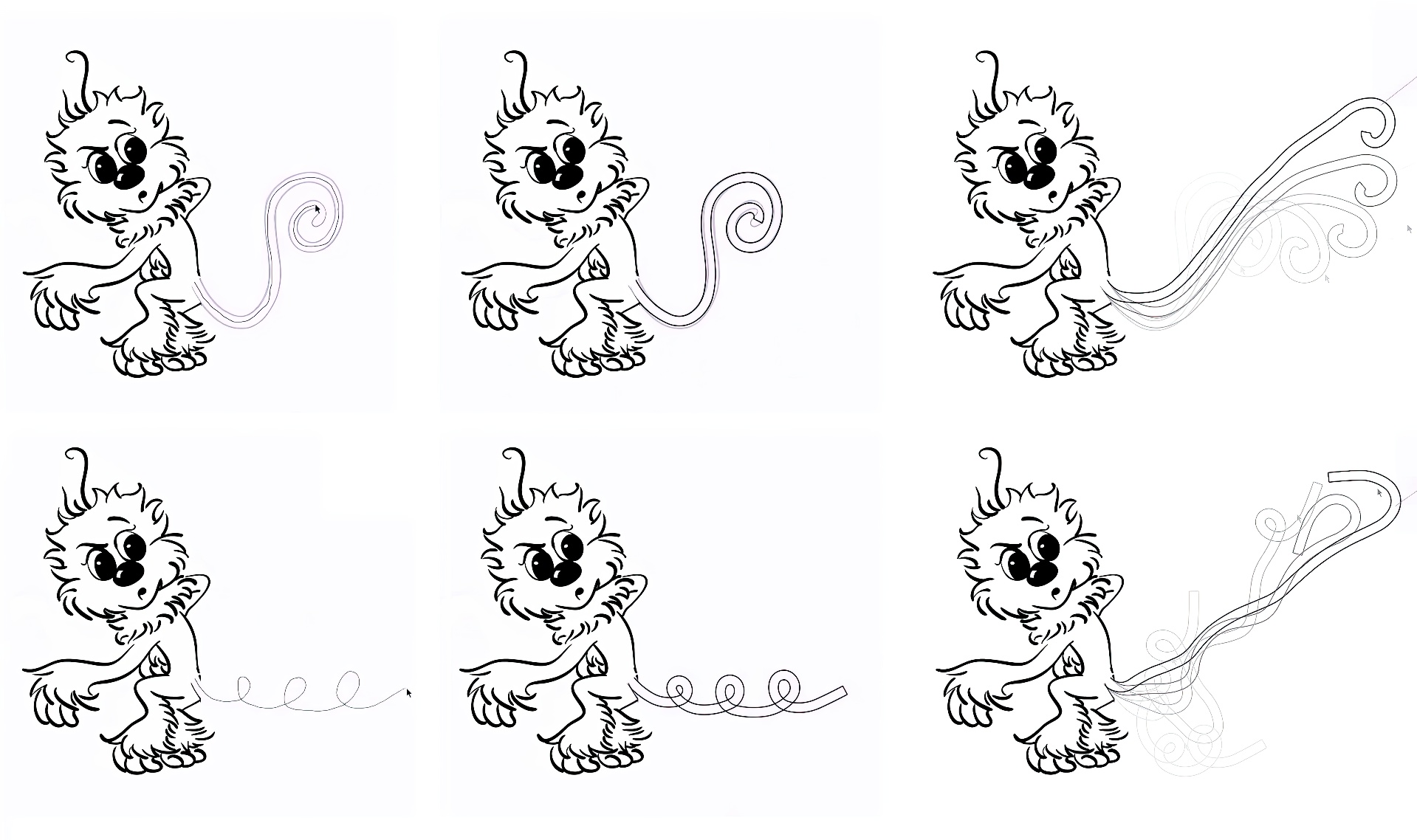
“Stable inverse dynamic curves”
Conference:
Type(s):
Title:
- Stable inverse dynamic curves
Session/Category Title: Curves, characters & crowds
Presenter(s)/Author(s):
Moderator(s):
Abstract:
2d animation is a traditional but fascinating domain that has recently regained popularity both in animated movies and video games. This paper introduces a method for automatically converting a smooth sketched curve into a 2d dynamic curve at stable equilibrium under gravity. The curve can then be physically animated to produce secondary motions in 2d animations or simple video games. Our approach proceeds in two steps. We first present a new technique to fit a smooth piecewise circular arcs curve to a sketched curve. Then we show how to compute the physical parameters of a dynamic rod model (super-circle) so that its stable rest shape under gravity exactly matches the fitted circular arcs curve. We demonstrate the interactivity and controllability of our approach on various examples where a user can intuitively setup efficient and precise 2d animations by specifying the input geometry.
References:
1. Alexa, M., Cohen-Or, D., and Levin, D. 2000. As-rigid-as-possible shape interpolation. In Computer Graphics Proceedings (Proceedings of the ACM SIGGRAPH’00 conference), ACM Press/Addison-Wesley Publishing Co., New York, NY, USA, ACM, 157–164. Google ScholarDigital Library
2. Alt, H., and Godau, M. 1995. Computing the fréchet distance between two polygonal curves. Internat. J. Comput. Geom. Appl. 5, 75–91.Google ScholarCross Ref
3. Baran, I., Lehtinen, J., and Popović, J. 2010. Sketching clothoid splines using shortest paths. Computer Graphics Forum (Proceedings of Eurographics’10). to appear.Google Scholar
4. Barbič, J., and Popović, J. 2008. Real-time control of physically based simulations using gentle forces. ACM Trans. on Graphics (SIGGRAPH Asia 2008) 27, 5, 163:1–163:10. Google ScholarDigital Library
5. Barzel, R. 1997. Faking dynamics of ropes and springs. IEEE Comput. Graph. Appl. 17, 3, 31–39. Google ScholarDigital Library
6. Baxter, W., Barla, P., and Anjyo, K.-I. 2009. N-way morphing for 2d animation. Computer Animation and Virtual Worlds (Proceedings of CASA) 20, 2. Google ScholarDigital Library
7. Bergou, M., Wardetzky, M., Robinson, S., Audoly, B., and Grinspun, E. 2008. Discrete elastic rods. ACM Transactions on Graphics (Proceedings of the ACM SIGGRAPH’08 conference) 27, 3, 1–12.Google Scholar
8. Bertails, F., Audoly, B., Querleux, B., Leroy, F., Lévêque, J.-L., and Cani, M.-P. 2005. Predicting natural hair shapes by solving the statics of flexible rods. In Eurographics’05 (short papers), J. Dingliana and F. Ganovelli, Eds., Eurographics. Eurographics’05 (short papers).Google Scholar
9. Bertails, F., Audoly, B., Cani, M.-P., Querleux, B., Leroy, F., and Lévêque, J.-L. 2006. Super-helices for predicting the dynamics of natural hair. In ACM Transactions on Graphics (Proceedings of the ACM SIGGRAPH’06 conference), ACM, 1180–1187. Google ScholarDigital Library
10. Bertails, F. 2009. Linear time super-helices. Computer Graphics Forum (Proceedings of Eurographics’09) 28, 2 (apr).Google Scholar
11. Bolton, K. 1975. Biarc curves. Journal of Computer Aided Design 7, 89–92.Google ScholarCross Ref
12. Drysdale, R. S., Rote, G., and Sturm, A. 2008. Approximation of an open polygonal curve with a minimum number of circular arcs and biarcs. Computational Geometry: Theory and Applications 41, 1–2, 31–47. Google ScholarDigital Library
13. Eiter, T., and Mannila, H. 1994. Computing discrete fréchet distance. Tech. rep., Technische Universitat Wien.Google Scholar
14. Featherstone, R. 1983. The calculation of robot dynamics using articulated-body inertias. International Journal of Robotics Research 2, 1, 13–30.Google ScholarCross Ref
15. Fulton, W. 2000. Eigenvalues, invariant factors, highest weights, and schubert calculus. Bull. Amer. Math. Soc 37, 209–249.Google ScholarCross Ref
16. Hadap, S. 2006. Oriented strands – dynamics of stiff multi-body system. In ACM SIGGRAPH – EG Symposium on Computer Animation (SCA’06), ACM-EG SCA, 91–100. Google ScholarDigital Library
17. Horng, J.-H. 2003. An adaptive smoothing approach for fitting digital planar curves with line segments and circular arcs. Pattern Recogn. Lett. 24, 1–3, 565–577.Google ScholarDigital Library
18. McCrae, J., and Singh, K. 2008. Sketching piecewise clothoid curves. Computers & Graphics 33, 4, 452–461. Google ScholarDigital Library
19. Nutbourne, A., and Martin, R. 1990. Differential Geometry applied fo Curve and Surface Design. Ellis Horwood.Google Scholar
20. Park, H. 2004. Optimal single biarc fitting and its applications. Computer-Aided Design and Applications 1, 1–4, 187–195.Google ScholarCross Ref
21. Pei, S.-C., and Horng, J.-H. 1996. Optimum approximation of digital planar curves using circular arcs. Pattern Recognition 29, 3, 383–388.Google ScholarCross Ref
22. Safonova, A., and Rossignac, J. 2003. Compressed piecewise-circular approximations of 3d curves. Computer-Aided Design 35, 6, 533–547.Google ScholarCross Ref
23. Selinger, P., 2003. Potrace: a polygon-based tracing algorithm. http://potrace.sourceforge.net/.Google Scholar
24. Selle, A., Lentine, M., and Fedkiw, R. 2008. A mass spring model for hair simulation. ACM Transactions on Graphics (Proceedings of the ACM SIGGRAPH’08 conference) 27, 3, 1–11. Google ScholarDigital Library
25. Spillmann, J., and Teschner, M. 2007. Corde: Cosserat rod elements for the dynamic simulation of one-dimensional elastic objects. In ACM SIGGRAPH – EG Symposium on Computer Animation (SCA’07), ACM-EG SCA, 63–72. Google ScholarDigital Library
26. Spillmann, J., and Teschner, M. 2008. An adaptive contact model for the robust simulation of knots. Computer Graphics Forum 27, 2. Proceedings of Eurographics’08.Google ScholarCross Ref
27. Theetten, A., Grisoni, L., Andriot, C., and Barsky, B. 2008. Geometrically exact splines. Journal of Computer Aided Design 40, 1, 35–48. Google ScholarDigital Library
28. Wither, J., Bertails, F., and Cani, M.-P. 2007. Realistic hair from a sketch. In International Conference on Shape Modeling and Applications, SMI 2007, June, 2007, IEEE, Lyon, France, IEEE, 33–42. Google ScholarDigital Library
29. Yang, S.-N., and Du, W.-C. 1996. Numerical methods for approximating digitized curves by piecewise circular arcs. J. Comput. Appl. Math. 66, 1–2, 557–569. Google ScholarDigital Library