“Quadrilateral mesh simplification”
Conference:
Type(s):
Title:
- Quadrilateral mesh simplification
Session/Category Title: Mesh processing
Presenter(s)/Author(s):
Abstract:
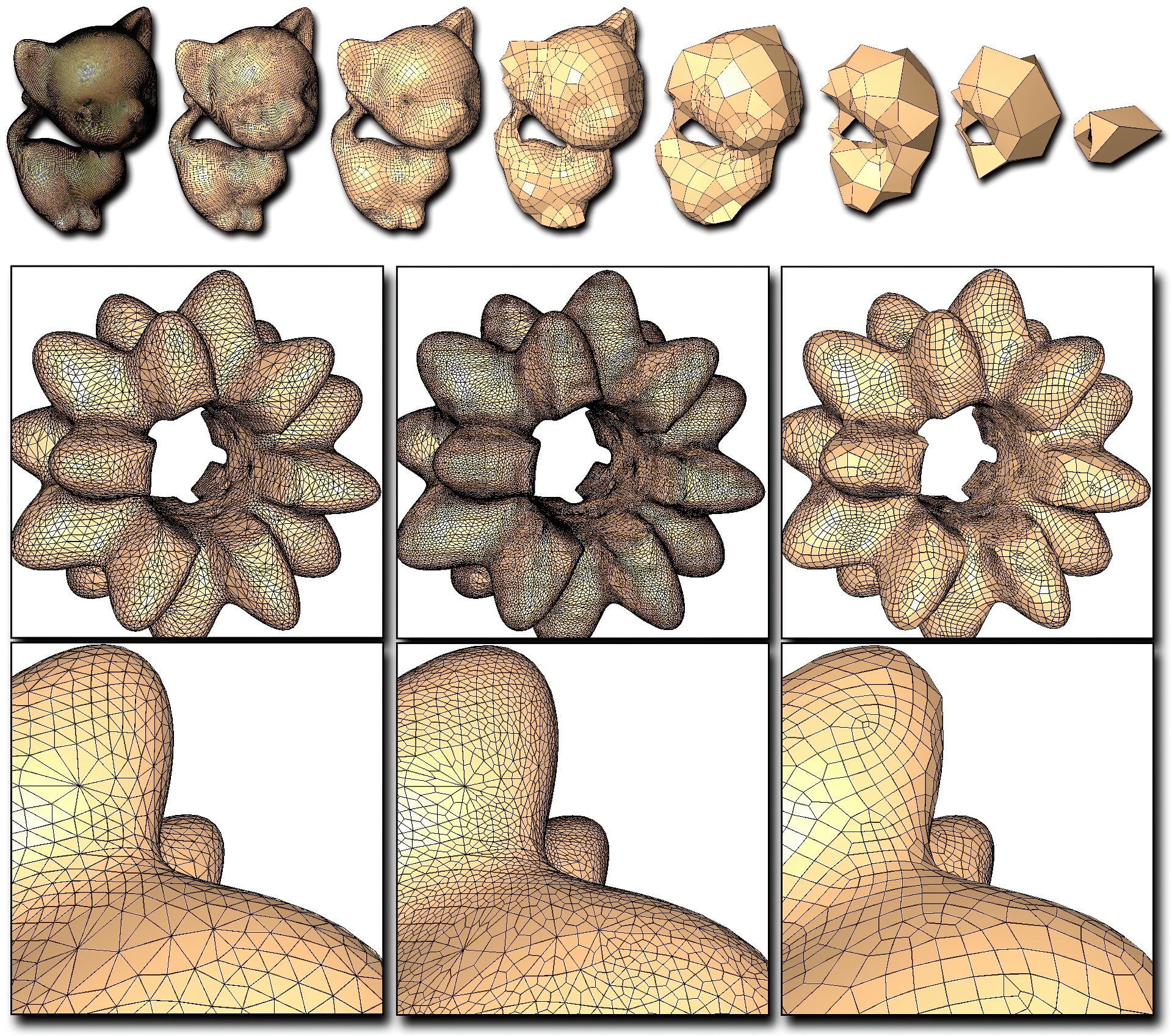
We introduce a simplification algorithm for meshes composed of quadrilateral elements. It is reminiscent of edge-collapse based methods for triangle meshes, but takes a novel approach to the challenging problem of maintaining the quadrilateral connectivity during level-of-detail creation. The method consists of a set of unit operations applied to the dual of the mesh, each designed to improve mesh structure and maintain topological genus. Geometric shape is maintained by an extension of a quadric error metric to quad meshes. The technique is straightforward to implement and efficient enough to be applied to real-world models. Our technique can handle models with sharp features, and can be used to re-mesh general polygonal, i.e. tri- and quad-dominant, meshes into quadonly meshes.
References:
1. Alliez, P., Cohen-Steiner, D., Devillers, O., Lévy, B., and Desbrun, M. 2003. Anisotropic polygonal remeshing. In ACM SIGGRAPH, 485–493. Google Scholar
2. Blacker, T., and Stephenson, M. 1991. Paving: A new approach to automated quadrilateral mesh generation. International Journal for Numerical Methods in Engineering (May), 811–847.Google Scholar
3. Borden, M., Benzley, S., and Shepherd, J. 2002. Hexahedral sheet extraction. In 11th International Meshing Roundtable, 147–152.Google Scholar
4. Bremer, P., Porumbescu, S., Joy, K., and Hamann, B. 2002. Automatic semi-regular mesh construction from adaptive distance fields. Curve and Surface Fitting: Saint-Malo.Google Scholar
5. Catmull, E., and Clark, J. 1978. Recursively generated b-spline surfaces on arbitrary topological meshes. Computer Aided Design 10, 6, 350–355.Google ScholarCross Ref
6. Cignoni, P., Montani, C., and Scopigno, R. 1998. A comparison of mesh simplification algorithms. Computers and Graphics 22, 1 (February), 37–54.Google ScholarCross Ref
7. Cohen-Steiner, D., Alliez, P., and Desbrun, M. 2004. Variational shape approximation. In ACM SIGGRAPH, 905–914. Google Scholar
8. Dewey, M. 2008. Automated Quadrilateral Coarsening by Ring Collapse. Master’s thesis, Bringham Young University.Google Scholar
9. Dong, S., Kircher, S., and Garland, M. 2005. Harmonic functions for quadrilateral remeshing of arbitrary manifolds. Computer Aided Geometric Design 22, 5, 392–423. Google ScholarDigital Library
10. Dong, S., Bremer, P.-T., Garland, M., Pascucci, V., and Hart, J. C. 2006. Spectral surface quadrangulation. In ACM SIGGRAPH, 1057–1066. Google Scholar
11. Eck, M., and Hoppe, H. 1996. Automatic reconstruction of b-spline surfaces of arbitrary topological type. In ACM SIGGRAPH, 325–334. Google Scholar
12. Edelsbrunner, H. 2006. Geometry and Topology for Mesh Generation. Cambridge University Press, New York, NY, USA. Google Scholar
13. Garland, M., and Heckbert, P. 1997. Surface simplification using quadric error metrics. In ACM SIGGRAPH, 209–216. Google Scholar
14. Guskov, I., Khodakovsky, A., Schröder, P., and Sweldens, W. 2002. Hybrid meshes: multiresolution using regular and irregular refinement. In ACM Symposium on Computational Geometry, 264–272. Google Scholar
15. Hoppe, H. 1999. New quadric metric for simplifying meshes with appearance attributes. In IEEE Visualization, 56–66. Google Scholar
16. Kalberer, F., Nieser, M., and Polthier, K. 2007. Quadcover: Surface parameterization using branched coverings. Computer Graphics Forum 26, 3, 375–384.Google ScholarCross Ref
17. Kinney, P. 1997. Cleanup: Improving quadrilateral finite element meshes. In 6th International Meshing Roundtable, 437–447.Google Scholar
18. Kobbelt, L. 1996. Interpolatory subdivision on open quadrilateral nets with arbitrary topology. Computer Graphics Forum 15, 3, 409–420.Google ScholarCross Ref
19. Krishnamurthy, V., and Levoy, M. 1996. Fitting smooth surface to dense polygon meshes. In ACM SIGGRAPH, 313–324. Google Scholar
20. Lai, Y.-K., Kobbelt, L., and Hu, S.-M. 2008. An incremental approach to feature aligned quad dominant remeshing. In ACM Solid and Physical Modeling Symposium. Google Scholar
21. Lindstrom, P., and Silva, C. 2001. A memory insensitive technique for large model simplification. In IEEE Visualization, 121–126. Google Scholar
22. Lindstrom, P. 2002. Out-of-core simplification of large polygonal meshes. In ACM SIGGRAPH, 259–262. Google Scholar
23. Luebke, D., Watson, B., Cohen, J. D., Reddy, M., and Varshney, A. 2002. Level of Detail for 3D Graphics. Elsevier Science Inc., New York, NY, USA. Google Scholar
24. Marinov, M., and Kobbelt, L. 2004. Direct anisotropic quaddominant remeshing. In Pacific Graphics, 207–216. Google Scholar
25. Marinov, M., and Kobbelt, L. 2006. A robust two-step procedure for quad-dominant remeshing. Computer Graphics Forum 25, 3, 537–546.Google ScholarCross Ref
26. Murdoch, P., Benzley, S., Blacker, T., and Mitchell, S. 1997. The spatial twist continuum: A connectivity based method for representing all-hexahedral finite element meshes. Finite Element in Analysis and Design 28, 2 (December), 137–149. Google ScholarDigital Library
27. Ni, X., Garland, M., and Hart, J. C. 2004. Fair morse functions for extracting the topological structure of a surface mesh. In ACM SIGGRAPH, 613–622. Google Scholar
28. Owen, S., Staten, M., Canann, S., and Saigal, S. 1999. Q-morph: An indirect approach to advancing front quad meshing. International Journal for Numerical Methods in Engineering (March), 1317–1340.Google Scholar
29. Shepherd, J. 2007. Topologic and Geometric Constraint-Based Hexahedral Mesh Generation. PhD thesis, University of Utah. Google Scholar
30. Shimada, K., and Gossard, D. C. 1995. Bubble mesh: automated triangular meshing of non-manifold geometry by sphere packing. In 3rd ACM Symposium on Solid Modeling and Applications, 409–419. Google Scholar
31. Shimada, K. 1993. Physically-based mesh generation: automated triangulation of surfaces and volumes via bubble packing. PhD thesis, Massachusetts Institute of Technology. Google Scholar
32. Shimada, K. 1999. Quadrilateral meshing with directionality control via close packing of square cells. SIAM Conference on Geometric Modeling.Google Scholar
33. Smith, J., and Boier-Martin, I. 2005. Combining metrics for mesh simplification and parameterization. In ACM SIGGRAPH Sketches, 135. Google Scholar
34. Staten, M. L., and Canann, S. A. 1997. Post refinement element shape improvement for quadrilateral meshes. ASME AMD: Trends in Unstructured Mesh Generation, 9–16.Google Scholar
35. Staten, M., Benzley, S., and Scott, M. 2008. A methodology for quadrilateral finite element mesh coarsening. Engineering with Computers, 241–251. Google Scholar
36. Takeuchi, S., Suzuki, H., Kimura, F., Kanai, T., and Shimada, K. 2000. Subdivision surface fitting with qem-based mesh simplification and reconstruction of approximated b-spline surfaces. In Pacific Graphics, 202. Google Scholar
37. Tong, Y., Alliez, P., Cohen-Steiner, D., and Desbrun, M. 2006. Designing quadrangulations with discrete harmonic forms. In Symposium on Geometry Processing, 201–210. Google ScholarDigital Library
38. Viswanath, N., Shimada, K., and Itoh, T. 2000. Quadrilateral meshing with anisotropy and directionality control via close packing of rectangular cells. In 9th International Meshing Roundtable, 227–238.Google Scholar
39. Zhang, Y., Bajaj, C., and Guoliang, X. 2005. Surface smoothing and quality improvement of quadrilateral/hexahedral meshes with geometric flow. In 14th International Meshing Roundtable, 449–468.Google Scholar