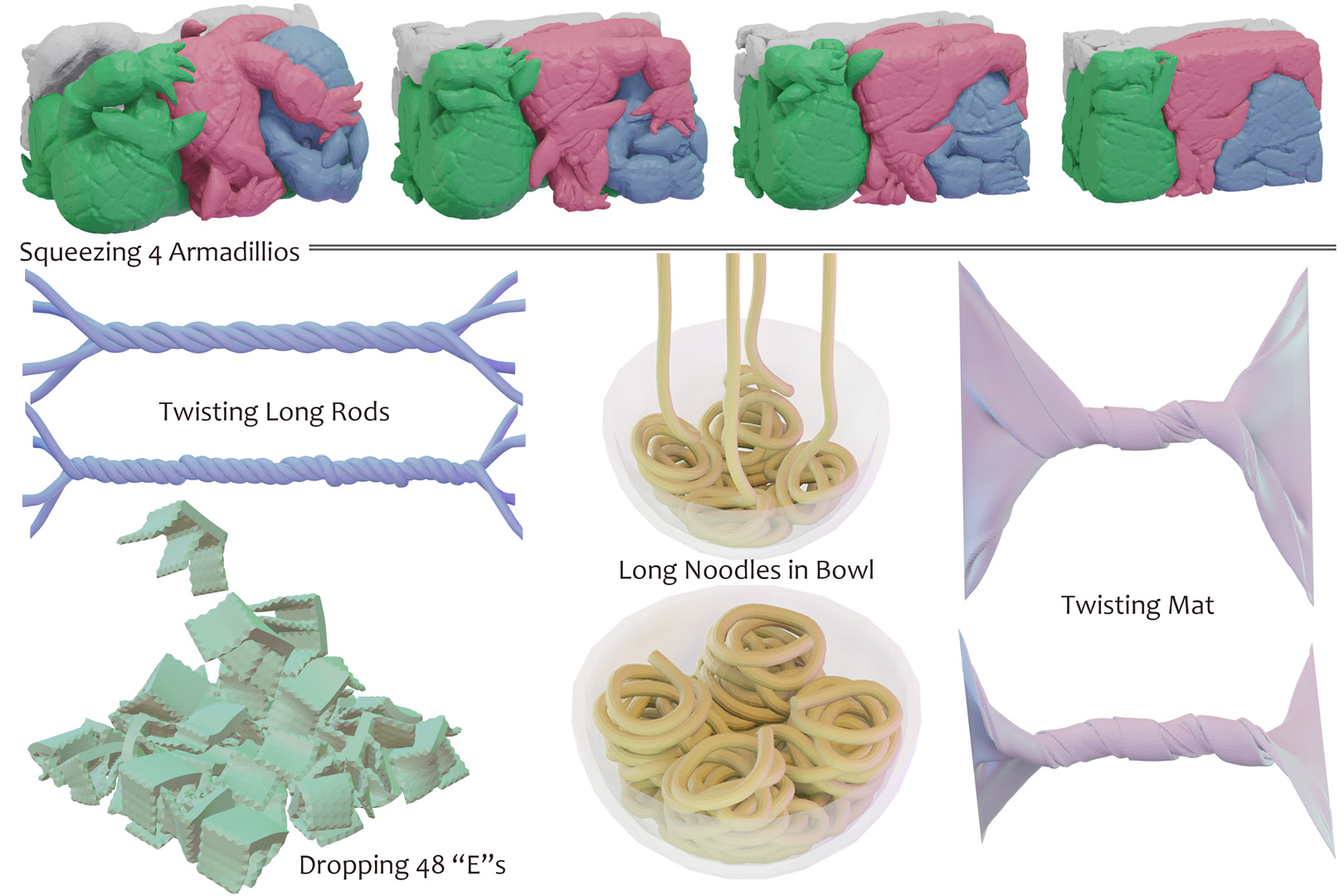
“Preconditioned Nonlinear Conjugate Gradient Method for Real-time Interior-point Hyperelasticity”
Conference:
Type(s):
Title:
- Preconditioned Nonlinear Conjugate Gradient Method for Real-time Interior-point Hyperelasticity
Presenter(s)/Author(s):
Abstract:
A preconditioned nonlinear conjugate gradient method is proposed for real-time simulation of elastic deformation with incremental potential contact. This method is GPU-parallelizable and demonstrates fast convergence. A line search strategy is proposed to determine an appropriate step size and achieve realistic simulation in complex scenarios without any additional collision detection.
References:
[1]
Neculai Andrei. 2009. Acceleration of conjugate gradient algorithms for unconstrained optimization. Appl. Math. Comput. 213, 2 (2009), 361?369.
[2]
Neculai Andrei. 2013. Another conjugate gradient algorithm with guaranteed descent and conjugacy conditions for large-scale unconstrained optimization. Journal of Optimization Theory and Applications 159 (2013), 159?182.
[3]
Neculai Andrei 2020. Nonlinear conjugate gradient methods for unconstrained optimization. Springer.
[4]
Jonathan Barzilai and Jonathan M Borwein. 1988. Two-point step size gradient methods. IMA journal of numerical analysis 8, 1 (1988), 141?148.
[5]
Mikl?s Bergou, Max Wardetzky, Stephen Robinson, Basile Audoly, and Eitan Grinspun. 2008. Discrete elastic rods. In ACM SIGGRAPH 2008 papers. 1?12.
[6]
Javier Bonet and Richard D. Wood. 2008. Nonlinear Continuum Mechanics for Finite Element Analysis (2 ed.). Cambridge University Press. https://doi.org/10.1017/CBO9780511755446
[7]
Sofien Bouaziz, Sebastian Martin, Tiantian Liu, Ladislav Kavan, and Mark Pauly. 2014. Projective dynamics. ACM Transactions on Graphics 33 (07 2014), 1?11. https://doi.org/10.1145/2601097.2601116
[8]
Min Gyu Choi and Hyeong-Seok Ko. 2005. Modal warping: Real-time simulation of large rotational deformation and manipulation. IEEE Transactions on Visualization and Computer Graphics 11, 1 (2005), 91?101.
[9]
Yu-Hong Dai and Cai-Xia Kou. 2013. A nonlinear conjugate gradient algorithm with an optimal property and an improved Wolfe line search. SIAM Journal on Optimization 23, 1 (2013), 296?320.
[10]
Kenny Erleben. 2018. Methodology for Assessing Mesh-Based Contact Point Methods. ACM Trans. Graph. 37, 3, Article 39 (jul 2018), 30 pages. https://doi.org/10.1145/3096239
[11]
Yu Fang, Minchen Li, Chenfanfu Jiang, and Danny M Kaufman. 2021. Guaranteed globally injective 3D deformation processing. ACM Transactions on Graphics 40, 4 (2021).
[12]
Zachary Ferguson, Minchen Li, Teseo Schneider, Francisca Gil-Ureta, Timothy Langlois, Chenfanfu Jiang, Denis Zorin, Danny M Kaufman, and Daniele Panozzo. 2021. Intersection-free rigid body dynamics. ACM Transactions on Graphics 40, 4 (2021).
[13]
Roger Fletcher. 2000. Practical methods of optimization. John Wiley & Sons.
[14]
Reeves Fletcher and Colin M Reeves. 1964. Function minimization by conjugate gradients. The computer journal 7, 2 (1964), 149?154.
[15]
William W Hager and Hongchao Zhang. 2005. A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM Journal on optimization 16, 1 (2005), 170?192.
[16]
Yuanming Hu, Tzu-Mao Li, Luke Anderson, Jonathan Ragan-Kelley, and Fr?do Durand. 2019. Taichi: a language for high-performance computation on spatially sparse data structures. ACM Transactions on Graphics (TOG) 38, 6 (2019), 1?16.
[17]
Couro Kane, Eduardo A Repetto, Michael Ortiz, and Jerrold E Marsden. 1999. Finite element analysis of nonsmooth contact. Computer methods in applied mechanics and engineering 180, 1-2 (1999), 1?26.
[18]
Danny M Kaufman, Shinjiro Sueda, Doug L James, and Dinesh K Pai. 2008. Staggered projections for frictional contact in multibody systems. In ACM SIGGRAPH Asia 2008 papers. 1?11.
[19]
Theodore Kim and David Eberle. 2022. Dynamic deformables: implementation and production practicalities (now with code!). In ACM SIGGRAPH 2022 Courses. 1?259.
[20]
Lei Lan, Danny M. Kaufman, Minchen Li, Chenfanfu Jiang, and Yin Yang. 2022a. Affine body dynamics: fast, stable and intersection-free simulation of stiff materials. 41, 4, Article 67 (jul 2022), 14 pages. https://doi.org/10.1145/3528223.3530064
[21]
Lei Lan, Minchen Li, Chenfanfu Jiang, Huamin Wang, and Yin Yang. 2023. Second-order Stencil Descent for Interior-point Hyperelasticity. ACM Trans. Graph. 42, 4, Article 108 (jul 2023), 16 pages. https://doi.org/10.1145/3592104
[22]
Lei Lan, Guanqun Ma, Yin Yang, Changxi Zheng, Minchen Li, and Chenfanfu Jiang. 2022b. Penetration-free projective dynamics on the GPU. ACM Transactions on Graphics (TOG) 41, 4 (2022), 1?16.
[23]
Lei Lan, Yin Yang, Danny Kaufman, Junfeng Yao, Minchen Li, and Chenfanfu Jiang. 2021. Medial IPC: accelerated incremental potential contact with medial elastics. ACM Transactions on Graphics 40, 4 (2021).
[24]
Minchen Li, Zachary Ferguson, Teseo Schneider, Timothy R Langlois, Denis Zorin, Daniele Panozzo, Chenfanfu Jiang, and Danny M Kaufman. 2020. Incremental potential contact: intersection-and inversion-free, large-deformation dynamics.ACM Trans. Graph. 39, 4 (2020), 49.
[25]
Minchen Li, Danny M. Kaufman, and Chenfanfu Jiang. 2021. Codimensional Incremental Potential Contact. ACM Trans. Graph. (SIGGRAPH) 40, 4, Article 170 (2021).
[26]
Xuan Li, Yu Fang, Lei Lan, Huamin Wang, Yin Yang, Minchen Li, and Chenfanfu Jiang. 2023. Subspace-Preconditioned GPU Projective Dynamics with Contact for Cloth Simulation. In SIGGRAPH Asia 2023 Conference Papers. 1?12.
[27]
Xuan Li, Yu Fang, Minchen Li, and Chenfanfu Jiang. 2022. BFEMP: Interpenetration-free MPM?FEM coupling with barrier contact. Computer Methods in Applied Mechanics and Engineering 390 (2022), 114350.
[28]
Tiantian Liu, Sofien Bouaziz, and Ladislav Kavan. 2017. Quasi-newton methods for real-time simulation of hyperelastic materials. Acm Transactions on Graphics (TOG) 36, 3 (2017), 1?16.
[29]
Zexian Liu and Hongwei Liu. 2018. Several efficient gradient methods with approximate optimal stepsizes for large scale unconstrained optimization. J. Comput. Appl. Math. 328 (2018), 400?413.
[30]
Ran Luo, Weiwei Xu, Tianjia Shao, Hongyi Xu, and Yin Yang. 2019. Accelerated complex-step finite difference for expedient deformable simulation. ACM Transactions on Graphics (TOG) 38, 6 (2019), 1?16.
[31]
Miles Macklin, Matthias M?ller, and Nuttapong Chentanez. 2016. XPBD: position-based simulation of compliant constrained dynamics. In Proceedings of the 9th International Conference on Motion in Games. 49?54.
[32]
Sanjay Mehrotra. 1992. On the implementation of a primal-dual interior point method. SIAM Journal on optimization 2, 4 (1992), 575?601.
[33]
Ullrich Meier, Oscar L?pez, Carlos Monserrat, Mari C Juan, and M Alcaniz. 2005. Real-time deformable models for surgery simulation: a survey. Computer methods and programs in biomedicine 77, 3 (2005), 183?197.
[34]
Matthias M?ller, matthimf, Johnathon Selstad, Thomas Oberbichler, and Elliot Waite. 2023. matthias-research/pages. https://github.com/matthias-research/pages
[35]
Jorge Nocedal and Stephen J Wright. 1999. Numerical optimization. Springer.
[36]
Elijah Polak and Gerard Ribiere. 1969. Note sur la convergence de m?thodes de directions conjugu?es. Revue fran?aise d?informatique et de recherche op?rationnelle. S?rie rouge 3, 16 (1969), 35?43.
[37]
Boris Teodorovich Polyak. 1969. The conjugate gradient method in extremal problems. U. S. S. R. Comput. Math. and Math. Phys. 9, 4 (1969), 94?112.
[38]
V Popescu, Grigore Burdea, and Mourad Bouzit. 1999. Virtual reality simulation modeling for a haptic glove. In Proceedings Computer Animation 1999. IEEE, 195?200.
[39]
Breannan Smith, Fernando De Goes, and Theodore Kim. 2018. Stable neo-hookean flesh simulation. ACM Transactions on Graphics (TOG) 37, 2 (2018), 1?15.
[40]
Joseph Teran, Eftychios Sifakis, Geoffrey Irving, and Ronald Fedkiw. 2005. Robust quasistatic finite elements and flesh simulation. In Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer animation. 181?190.
[41]
Demetri Terzopoulos and Kurt Fleischer. 1988. Deformable models. The visual computer 4, 6 (1988), 306?331.
[42]
Demetri Terzopoulos, John Platt, Alan Barr, and Kurt Fleischer. 1987. Elastically deformable models. In Proceedings of the 14th annual conference on Computer graphics and interactive techniques. 205?214.
[43]
Demetri Terzopoulos, Andrew Witkin, and Michael Kass. 1988. Constraints on deformable models: Recovering 3D shape and nonrigid motion. Artificial intelligence 36, 1 (1988), 91?123.
[44]
Takuya Umedachi, Vishesh Vikas, and Barry A Trimmer. 2013. Highly deformable 3-D printed soft robot generating inching and crawling locomotions with variable friction legs. In 2013 IEEE/RSJ international conference on Intelligent Robots and Systems. IEEE, 4590?4595.
[45]
Mickeal Verschoor and Andrei C Jalba. 2019. Efficient and accurate collision response for elastically deformable models. ACM Transactions on Graphics (TOG) 38, 2 (2019), 1?20.
[46]
Huamin Wang. 2018. Rule-free sewing pattern adjustment with precision and efficiency. ACM Transactions on Graphics (TOG) 37, 4 (2018), 1?13.
[47]
Huamin Wang and Yin Yang. 2016. Descent methods for elastic body simulation on the GPU. ACM Transactions on Graphics (TOG) 35, 6 (2016), 1?10.
[48]
Tianyu Wang, Jiong Chen, Dongping Li, Xiaowei Liu, Huamin Wang, and Kun Zhou. 2023. Fast GPU-Based Two-Way Continuous Collision Handling. ACM Transactions on Graphics 42, 5 (2023), 1?15.
[49]
Tianyi Xie, Minchen Li, Yin Yang, and Chenfanfu Jiang. 2023. A Contact Proxy Splitting Method for Lagrangian Solid-Fluid Coupling. ACM Transactions on Graphics (TOG) 42, 4 (2023), 1?14.
[50]
Chang Yu, Yi Xu, Ye Kuang, Yuanming Hu, and Tiantian Liu. 2022. MeshTaichi: A Compiler for Efficient Mesh-Based Operations. ACM Trans. Graph. 41, 6, Article 252 (nov 2022), 17 pages. https://doi.org/10.1145/3550454.3555430
[51]
Yidong Zhao, Jinhyun Choo, Yupeng Jiang, Minchen Li, Chenfanfu Jiang, and Kenichi Soga. 2022. A barrier method for frictional contact on embedded interfaces. Computer Methods in Applied Mechanics and Engineering 393 (2022), 114820.