“In the Quest for Scale-Optimal Mappings”
Conference:
Type(s):
Title:
- In the Quest for Scale-Optimal Mappings
Presenter(s)/Author(s):
Abstract:
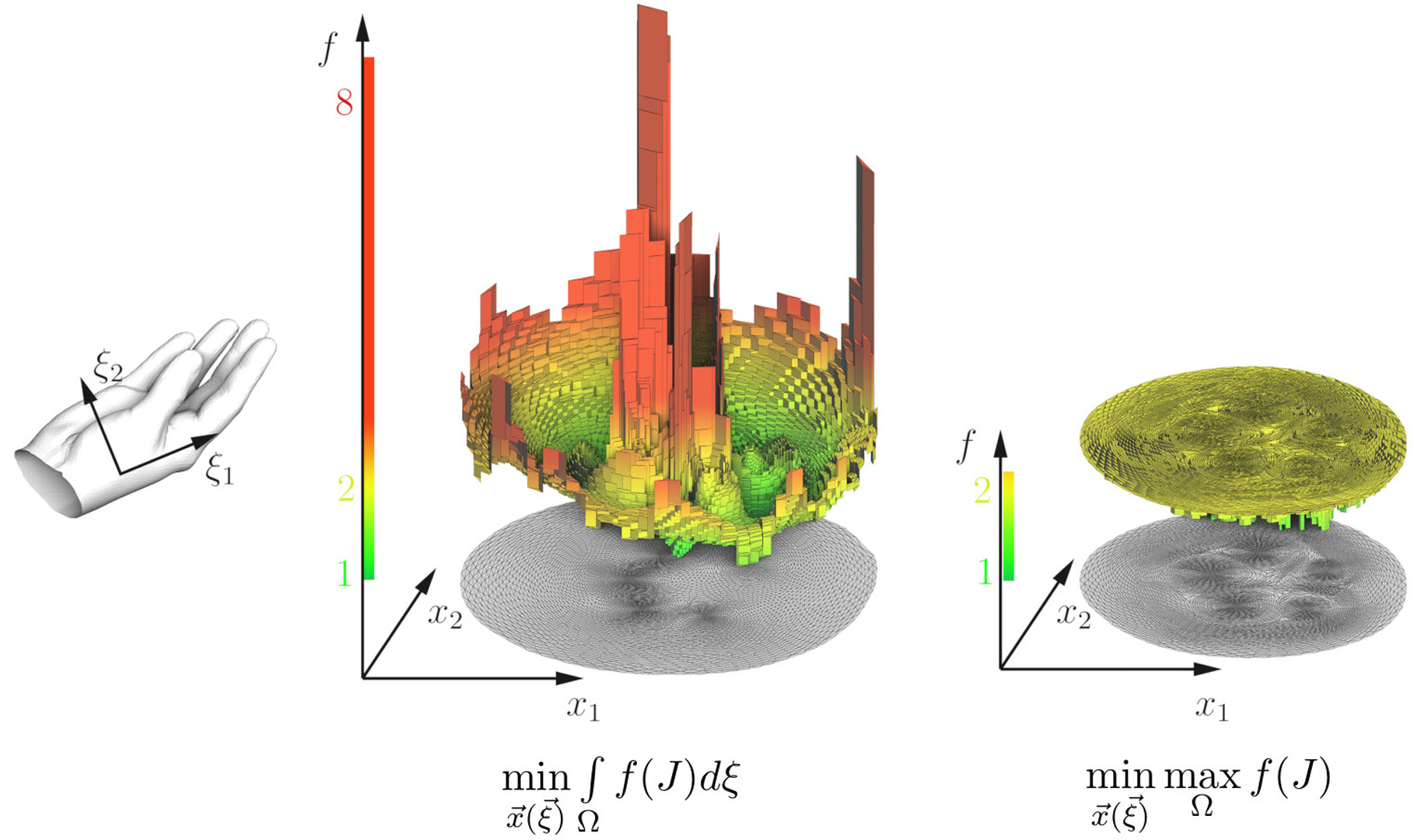
We present an algorithm for the max-norm minimization of hyperelastic distortion for mesh deformation.
Under certain conditions our method can build a deformation whose maximum distortion is arbitrarily close to the (unknown) minimum.
In summary, we reliably build 2D and 3D mesh deformations with the smallest known distortion estimates.
References:
[1]
Noam Aigerman and Yaron Lipman. 2013. Injective and bounded distortion mappings in 3D. ACM Trans. Graph. 32, 4, Article 106 (July2013), 14 pages. DOI:
[2]
Erling D. Andersen and Knud D. Andersen. 2000. The Mosek Interior Point Optimizer for Linear Programming: An Implementation of the Homogeneous Algorithm. Springer US, Boston, MA, 197?232. DOI:
[3]
Nikolai Sergeevich Bakhvalov. 1969. The optimization of methods of solving boundary value problems with a boundary layer. USSR Comput. Math. Math. Phys. 9 (1969), 139?166.
[4]
John M. Ball. 1976. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63, 4 (1976), 337?403.
[5]
David Bommes, Henrik Zimmer, and Leif Kobbelt. 2009. Mixed-integer quadrangulation. ACM Trans. Graph. 28, 3, Article 77 (July2009), 10 pages. DOI:
[6]
Mario Bonk and Urs Lang. 2003. Bi-Lipschitz parameterization of surfaces. Math. Ann. 327, 1 (2003), 135?169.
[7]
Pafnuty Lvovich Chebyshev. 1856. Sur la construction des cartes g?ographiques. Bulletin de la classe physico-math?matique de l?Acad?mie Imp?riale des sciences de Saint-P?tersbourg VIV (1856), 257?261. Reprinted in P. L. Tchebychef, ?uvres I, Chelsea, New York, 1962, pp. 233?236 and 239?247.
[8]
Edward Chien, Zohar Levi, and Ofir Weber. 2016. Bounded distortion parametrization in the space of metrics. ACM Trans. Graph. 35, 6, Article 215 (Nov.2016), 16 pages. DOI:
[9]
P. G. Ciarlet and G. Geymonat. 1982. Sur les lois de comportement en elasticite non-lineaire compressible. C.R. Acad. Sci. Paris Ser.II 295 (1982), 423?426.
[10]
Philippe Ciarlet and Jindrich Necas. 1985. Unilateral problems in nonlinear, three-dimensional elasticity. Arch. Rational Mech. Anal. 87 (1985), 319?338. DOI:
[11]
Philippe G. Ciarlet. 1988. Mathematical Elasticity: Three-Dimensional Elasticity. Number v. 1 in Studies in mathematics and its applications. North-Holland.
[12]
Carl de Boor. 1973. Good Approximation by Splines with Variable Knots. Birkh?user, Basel, 57?72. DOI:
[13]
A. Dinchenko. 1938. Chebyshev projection for the Soviet Union (in Russian). Geodesist 10 (1938), 4?14. Retrieved from https://elib.rgo.ru/safe-view/123456789/222079/1/MDAwMDAzMDZfR2VvZGV6aXN0IOKEljEwLnBkZg==
[14]
Xingyi Du, Noam Aigerman, Qingnan Zhou, Shahar Z. Kovalsky, Yajie Yan, Danny M. Kaufman, and Tao Ju. 2020. Lifting simplices to find injectivity. ACM Trans. Graph. 39, 4, Article 120 (July2020), 17 pages. DOI:
[15]
G. B. Airy Esq.1861. LIII. Explanation of a projection by balance of errors for maps applying to a very large extent of the earth?s surface; and comparison of this projection with other projections. London, Edinburgh, Dublin Philos. Mag. J. Sci. 22, 149 (1861), 409?421. DOI:
[16]
Yu Fang, Minchen Li, Chenfanfu Jiang, and Danny M. Kaufman. 2021. Guaranteed globally injective 3D deformation processing. ACM Trans. Graph. (SIGGRAPH) 40, 4, Article 75 (2021).
[17]
Xiao-Ming Fu and Yang Liu. 2016. Computing inversion-free mappings by simplex assembly. ACM Trans. Graph. 35, 6, Article 216 (Nov.2016), 12 pages. DOI:
[18]
Xiao-Ming Fu, Yang Liu, and Baining Guo. 2015. Computing locally injective mappings by advanced MIPS. ACM Trans. Graph. 34, 4, Article 71 (July2015), 12 pages. DOI:
[19]
Vladimir Garanzha. 2000. The barrier method for constructing quasi-isometric grids. Comput. Math. Math. Phys. 40 (2000), 1617?1637.
[20]
Vladimir Garanzha and Igor Kaporin. 1999. Regularization of the barrier variational method of grid generation. Comput. Math. Math. Phys. 39, 9 (1999), 1426?1440.
[21]
Vladimir Garanzha, Igor Kaporin, Liudmila Kudryavtseva, Fran?ois Protais, Nicolas Ray, and Dmitry Sokolov. 2021. Foldover-free maps in 50 lines of code. ACM Trans. Graph. 40, 4 (2021). DOI:
[22]
Vladimir Garanzha and Liudmila Kudryavtseva. 2019. Hypoelastic stabilization of variational algorithm for construction of moving deforming meshes. In Optimization and Applications, Yury Evtushenko, Milojica Ja?imovi?, Michael Khachay, Yury Kochetov, Vlasta Malkova, and Mikhail Posypkin (Eds.). Springer International Publishing, Cham, 497?511.
[23]
Vladimir Garanzha, Liudmila Kudryavtseva, and Sergei Utyuzhnikov. 2014. Variational method for untangling and optimization of spatial meshes. J. Comput. Appl. Math. 269 (2014), 24?41. DOI:
[24]
Sergei Konstantinovich Godunov, Valerii Mikhailovich Gordienko, and Gennadii Aleksandrovich Chumakov. 1994. Quasi-isometric parametrization of a curvilinear quadrangle and a metric of constant curvature. Matematicheskie Trudy 26 (1994), 3?19.
[25]
Demetrius Grav?. 1911. D?monstration d?un th?or?me de Tch?bychef g?n?ralis? (in French). Journal f?r die reine und angewandte Mathematik 140 (1911), 247?251.
[26]
Magnus R. Hestenes and Eduard Stiefel. 1952. Methods of conjugate gradients for solving linear systems. J. Res. Natl. Bureau Stand. 49 (1952), 409?435.
[27]
K. Hormann and G. Greiner. 2000. MIPS: An efficient global parametrization method. In Curve and Surface Design. Vanderbilt University Press.
[28]
Weizhang Huang. 2001. Variational mesh adaptation: Isotropy and equidistribution. J. Comput. Phys. 174, 2 (Dec.2001), 903?924. DOI:
[29]
S. A. Ivanenko. 2000. Control of cell shapes in the course of grid generation. Zh. Vychisl. Mat. Mat. Fiz. 40 (Jan. 2000), 1662?1684.
[30]
Olivier-P. Jacquotte. 1988. A mechanical model for a new grid generation method in computational fluid dynamics. Comput. Methods Appl. Mech. Eng. 66, 3 (1988), 323?338.
[31]
Shahar Z. Kovalsky, Noam Aigerman, Ronen Basri, and Yaron Lipman. 2014. Controlling singular values with semidefinite programming. ACM Trans. Graph. 33, 4 (2014). DOI:
[32]
Shahar Z. Kovalsky, Noam Aigerman, Ronen Basri, and Yaron Lipman. 2015. Large-scale bounded distortion mappings. ACM Trans. Graph. 34, 6 (2015).
[33]
Zohar Levi and Denis Zorin. 2014. Strict minimizers for geometric optimization. ACM Trans. Graph. 33, 6, Article 185 (Nov.2014), 14 pages. DOI:
[34]
Yaron Lipman. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Trans. Graph. 31, 4, Article 108 (July2012), 13 pages. DOI:
[35]
John Milnor. 1969. A problem in cartography. Amer. Math. Month. 76, 10 (1969), 1101?1112. http://www.jstor.org/stable/2317182
[36]
William Prager. 1957. On ideal locking materials. Trans. Soc. Rheol. 1, 1 (1957), 169?175.
[37]
Michael Rabinovich, Roi Poranne, Daniele Panozzo, and Olga Sorkine-Hornung. 2017. Scalable locally injective mappings. ACM Trans. Graph. 36, 2, Article 16 (Apr.2017), 16 pages. DOI:
[38]
Yu G. Reshetnyak. 1966. Bounds on moduli of continuity for certain mappings. Siberian Math. J. 7, 5 (1966), 879?886.
[39]
Martin Rumpf. 1996. A variational approach to optimal meshes. Numer. Math. 72, 4 (1996), 523?540.
[40]
Christian Sch?ller, Ladislav Kavan, Daniele Panozzo, and Olga Sorkine-Hornung. 2013. Locally injective mappings. Comput. Graph. Forum 32, 5 (2013).
[41]
Olga Sorkine and Marc Alexa. 2007. As-Rigid-as-Possible surface modeling. In Proceedings of the 5th Eurographics Symposium on Geometry Processing (SGP?07). Eurographics Association, Goslar, DEU, 109?116.
[42]
O. Sorkine, D. Cohen-Or, R. Goldenthal, and D. Lischinski. 2002. Bounded-distortion piecewise mesh parameterization. In Proceedings of the IEEE Conference on Visualization (VIS?02).355?362. DOI:
[43]
Jian-Ping Su, Xiao-Ming Fu, and Ligang Liu. 2019. Practical foldover-free volumetric mapping construction. Comput. Graph. Forum 38, 7 (2019), 287?297. DOI:arXiv:https://onlinelibrary.wiley.com/doi/pdf/ 10.1111/cgf.13837
[44]
P. L. Tchebychev. 1853. Th?orie des m?canismes connus sous le nom de parall?logrammes. Imprimerie de l?Acad?mie imp?riale des sciences.
[45]
X. Xu, Weizhang Huang, R. Russell, and J. Williams. 2011. Convergence of de Boor?s algorithm for the generation of equidistributing meshes. IMA J. Numer. Anal. 31 (Apr. 2011), 580?596. DOI:
[46]
C. Zhu, R. H. Byrd, and J. Nocedal. 1997. L-BFGS-B: Algorithm 778: L-BFGS-B, FORTRAN routines for large scale bound constrained optimization. ACM Trans. Math. Software 23, 4 (1997), 550?560.