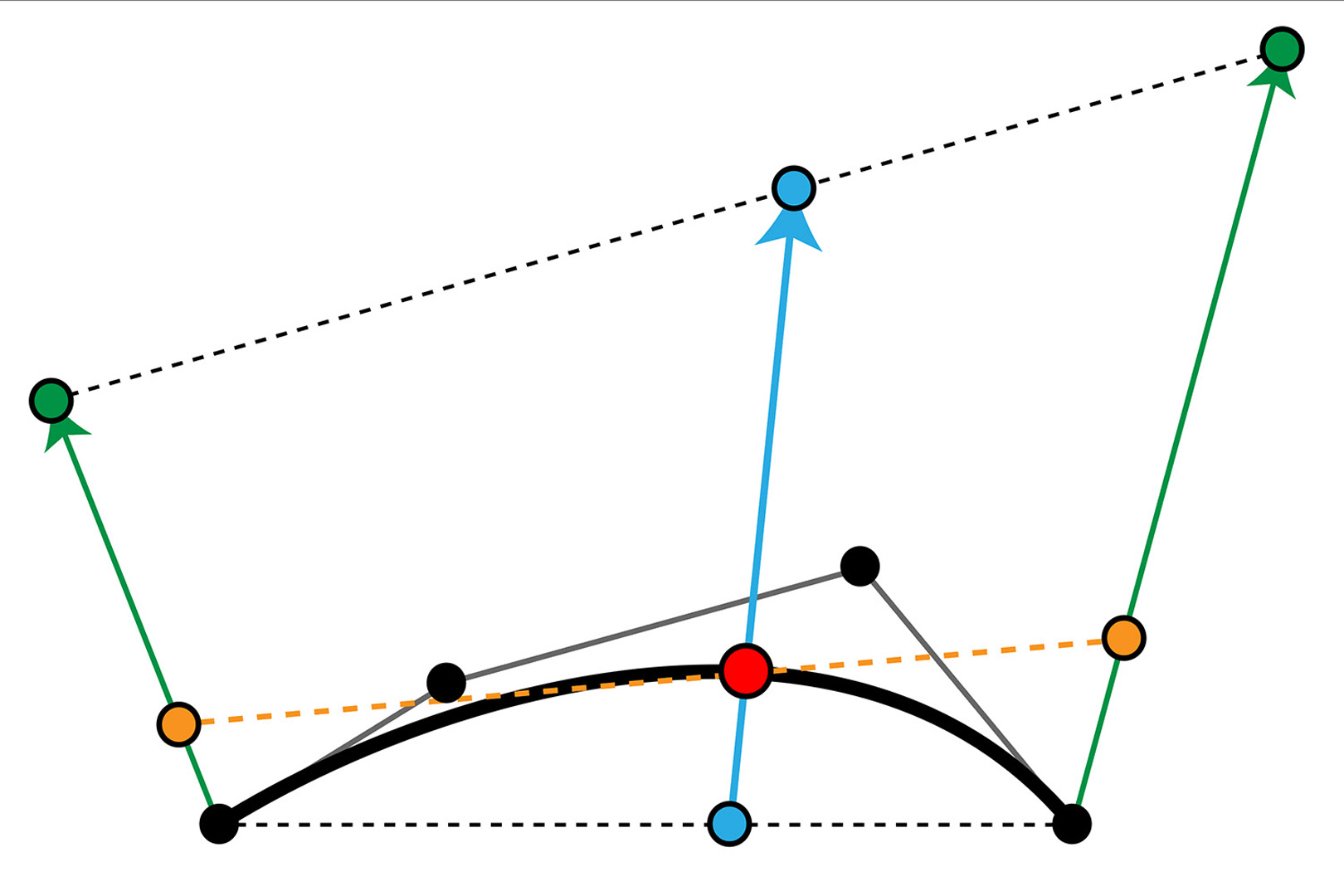
“Seiler’s Interpolation for Evaluating Polynomial Curves” by Yuksel
Conference:
Title:
- Seiler’s Interpolation for Evaluating Polynomial Curves
Session/Category Title: Less Work, More Perf
Presenter(s)/Author(s):
Abstract:
Seiler’s interpolation allows evaluating polynomial curves, such as Bézier curves, with a small number of linear interpolations. It is particularly effective with hardware linear interpolation used in GPU texture filtering. We compare it to the popular alternatives, such as de Casteljau’s algorithm, and present how it extends to higher-degree polynomials.
References:
[1]
Daqi Lin, Larry Seiler, and Cem Yuksel. 2021. Hardware Adaptive High-Order Interpolation for Real-Time Graphics. Computer Graphics Forum (Proceedings of HPG 2021) 40, 8 (2021), 1–16. https://doi.org/10.1111/cgf.14377
[2]
Cem Yuksel, Scott Schaefer, and John Keyser. 2011. Parameterization and Applications of Catmull-Rom Curves. Computer Aided Design 43, 7 (2011), 747–755. https://doi.org/10.1016/j.cad.2010.08.008